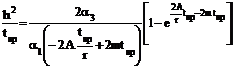|
||||||
|
|
Home| Journals | Statistics Online Expert | About Us | Contact Us | |||||
 |
||||||
| About this Journal | Table of Contents | ||||||
|
|
[Abstract] [PDF] [HTML] [Linked References] MHD Accelerated Motion on A Body Placed Symmetrical to the Flow in the Presence of A Transverse Magnetic Field Fixed Relative to the Fluid Mamta Goyal Department of Mathematics, University of Rajasthan, Jaipur-302055, Rajasthan, INDIA. Corresponding Addresses: Research Article Abstract: An analysis is performed for a two dimensional boundary layer flow of an electrically conducting fluid due to an unsteady external flow velocity, whose acceleration is governed by a power law, on a body placed symmetrical to the flow in the presence of an externally applied transverse magnetic field fixed relative to the fluid. The boundary layer equations have been solved by using a method previously developed by Bianchini, based on expressing the unknown velocity in terms of an error function and using differential and integral relations obtained from the governing equations. As an example, the impulsive flow past a circular cylinder is considered. The flow field is divided into two regions namely MHD Rayleigh region and MHD Blasius region. It is found that the effect of the magnetic field is to delay separation which stabilizes the flow. The results are in good agreement with the numerical data available in the literature. Key words: Magnetohydrodynamics, Boundary layer, Integral method.
1.0 Introduction Several authors like Bianchini [2], Berardi [3] and DeSocio [5] have studied in detail an approximate integral method for solving the unsteady laminar boundary layer equations for the flow of an electrically non-conducting fluid, with a wide range of initial and boundary conditions. Dass [6] has studied the numerical solution of mass transfer effects on an unsteady flow past an accelerated vertical porous plate with suction. The present paper is concerned with the MHD boundary layer flow due to an unsteady external flow whose acceleration is governed by power law, on a body placed symmetrically to the flow in the presence of an external applied transverse magnetic field fixed relative to the fluid. An integral method suggested by Bianchini [2] for non-conducting fluid flow is modified for solving the governing equations of MHD flow over a body. The distance traversed by the boundary layer before separation occurs is determined for an impulsive flow over a circular cylinder. It is found that effect of magnetic field is to delay boundary layer separation and thus stabilizes the flow. The results are in close agreement with those obtained by Dave [4] using Jeffreys and Jeffreys Hhn function. Jeffreys [7] explained in the book by Bansal [1].
2.0 Formulation of Problem. For constant fluid properties, the equations governing this type of MHD motion are
We are considering a two dimensional motion in a constant transverse magnetic field fixed relative to the fluid, therefore Physical configuration of the flow is shown in Fig.1.0. After applying the Prandtl boundary layer approximations the dimensional MHD-boundary layer equations may be written as where
Introducing the non-dimensional quantities as
The MHD-boundary layer equations (2.5) using (2.6) and (2.7) may be written in the non-dimensional form as
The quantities with subscript ‘0’ are some characteristic values of the respective variables whereas the subscript ‘¥’ denotes the values at the edge of the boundary layer and other symbols have their usual meanings. The boundary and compatibility conditions are as follows:
Besides these boundary conditions (2.11) we shall need some initial conditions which will be discussed later. An integral formulation of the problem is obtained by the integration of the equation (2.9) with the help of (2.10) as
Here the subscripts denote the respective partial derivatives. The above integro-differential equation may be reduced to a partial differential equation of Lagrange’s form if we make the following assumption for the velocity profile: where h is a scaling function of the coordinate normal to the body. Thus the equation (2.12) reduces to
where
3.0 Method of Solution: Equation (2.14) is a first-order, linear partial differential equation in the unknown scalar function h(x,m,t) which corresponds the boundary layer thickness and the corresponding auxiliary equation of the above equation is
…(3.1) Let where F is the function to be determined from the initial conditions to be associated to the boundary conditions (2.11). From the first two members of equation (3.1) one has immediately
To determine f2, one considers the first and last members of equation (3.1), which on integration gives
where Finally,
…(3.5) The general integral (3.2) can then be expressed as
with
…(3.7) and which implies that t = t(s). The function F in equation (3.6) can be obtained with the help of following initial conditions:
The function F (x - s), in view of the initial conditions (3.9) and (3.10), may be written in terms of another function y (s - x) as
where U(x) is the unit function (= 0 for x < 0; = 1 for x > 0) We now observe the following properties of the function F (i) For x > s, s - x < 0 (ii) For x < s, s - x > 0 F (x - s) = y (s - x) Þ F (-s) = y(s). …(3.13) Putting x = 0 in equation (3.6) and using the condition (3.10), we get
By using (3.13)
Equation (3.6), with the help of equation (3.11) may now be written as
where the function f(m,t) and y(s) are defined by equation (3.7) and equation (3.14) respectively. 4.0 Application The asymptotic behaviour of the exact solution in the absence of the magnetic field for an accelerated motion over a body suggests the choice of f(z) as the error function where the constant ‘a’ is determined from (2.9) and (2.13) using the boundary conditions (2.11) at y = 0
and where h0 is a scaling function of the coordinate normal to the body in the absence of magnetic field. From equation (4.1), equation (2.13) becomes
4.1 Determination of H (x, m, t). Using the boundary conditions (2.11) in equation (3.15), we get
By the definition of U(x), the equation (4.5) reduces to
Further from equation (3.8), we obtain where f (m,t) is given by equation (3.7), F (x - s) from (3.11) and As an example we consider the impulsive flow over a circular cylinder of radius ‘r’ a = 0 and u¥ (x,m,t) = w(x) …(4.9) At the point of separation, we put and for a circular cylinder of radius ‘r’ in the neighbourhood of rear stagnation point, we have Using (4.9), (3.7), (4.3) and (4.11) in (4.6), we get
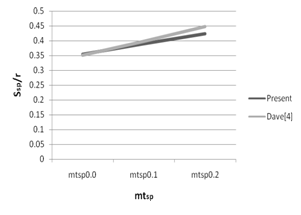
5.0 Numerical Discussion and Conclusion. Equation (3.15) shows that when the fluid is accelerated over a body placed symmetrical to the flow in the presence of transverse magnetic field fixed relative to the fluid, the flow field can be divided in two regions namely MHD Rayleigh region (x > s) and MHD Blasius region (x < s) with a singularity at the junction of the two regions. For MHD Rayleigh region ( x > s),the distance traversed by the boundary layer before separation for an impulsive flow on a circular cylinder of radius ‘r’, for small values of the magnetic interaction parameter mtsp is shown in fig 2.0 and the results are compared with Dave [4]. This clearly shows that the effect of the magnetic field is to delay separation which stabilizes the flow.
B0 Y
Fig.1.0. Physical configuration and co-ordinate system of MHD boundary layer on a body placed symmetrical to the flow in presence of transverse magnetic field fixed to the fluid.
Fig.2.0. Distance traversed by the boundary layer before separation occurs in an impulsive flow past a circular cylinder of radius ‘r’ in the presence of a transverse magnetic field fixed relative to the fluid.
Acknowledgement. The author is thankful to the Prof J.L.Bansal, for his valuable suggestions.
References
|
|||||
|
||||||
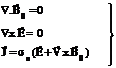
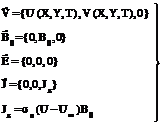
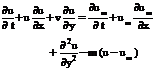
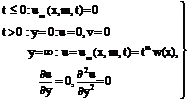
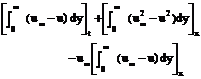
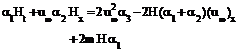
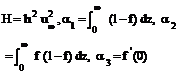
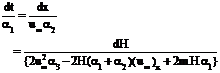
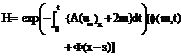
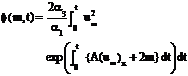
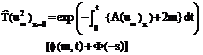
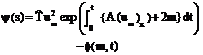 …(3.14)
…(3.14)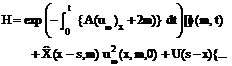
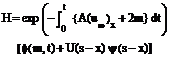
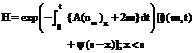 …(4.7)
…(4.7)