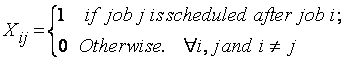|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Home| Journals | Statistical Calculator | About Us | Contact Us | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| About this Journal | Table of Contents | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
[Abstract] [PDF] [HTML] [Linked References]
Selection of Job Shop Scheduling Problem Using Fuzzy Linguistic Variables
Vikas S. Jadhav1 and V. H. Bajaj2 {1Research Student, 2Professor} Department of Statistics, Dr.B.A.M.University, Aurangabad-431004(M.S) INDIA. Corresponding Addresses: 1[email protected], 2[email protected] Research Article
Abstract: Job-shop scheduling (JSS) is a difficult problem, both theoretically and practically. The theoretical problems stem from the search for optimal schedules to a �Minimum /limited number of resources (Machines)� to complete the �Maximum works (Tasks)� with customers satisfaction. This paper, concentrates on JSS Problem under fuzzy approach to solve a real life tailor JSSP formulated. The scheduling problem is a very common problem of a tailor shop, such that we have to satisfy the multiple conflicting objectives, which are to �Minimize the job lateness or tardiness� and �Maximize the customer satisfaction� in the best possible manner. Here we try �to find out an optimal scheduling sequence to perform the jobs that arrive at the shop�. In this paper, the customer priority is based on the �fuzzy linguistic variables �It is expressed as Bad, Low, Medium, High, Very High etc. Fuzzy sets are used for modeling uncertainty due to vagueness. Fuzzy membership functions are used to define how well a value �fits� into a fuzzy set.A new technique is proposed based on the concept of fuzzy linguistic membership functions. This JSS model is more practical and realistic in manufacturing areas. Numerical example is given to demonstrate the effectiveness of the new developed model. Key Words: Job Shop Scheduling, Fuzzy Linguistic Variables, Optimal Scheduling, Fuzzy Sets, Vagueness.
1. Introduction
Scheduling consists of planning and arranging jobs in an orderly sequence of operations in order to �Meet the customer's requirements� [1]. The schedule of jobs and the control of their flows through a production process are the most significant role in any modern manufacturing systems. In a single machine scheduling, there is only one machine to process all jobs to optimize the objective function, say minimizing the sum of the maximum earliness and tardiness [2]. It is well known that the optimal solution of single objective models can be quite different to those models consist of multi objectives. In fact, the decision maker often wants to minimize the earliness/tardiness penalty or total flow time. Each of these objectives is valid from a general point of view. Since these objectives conflict with each other, a solution may perform well for one objective or it gives inferior results for others. For this reason, scheduling problems have a multi-objective nature. In decision making situations, the high degree of fuzziness and uncertainties are included in the data set. The fuzzy set theory provides a framework for handling the uncertainties of this type [3].Bellman and Zadeh [4] presented some applications of fuzzy theory to the various decision-making processes in a fuzzy environment. Zimmerman [5,6] presented a fuzzy optimization technique to a linear programming (LP) problem with single and multi-objectives. The fuzzy set theory has been applied to formulate and solve problems in various areas such as artificial intelligence, image processing, robotics, pattern recognition, (Hannan, [7] and Yager, [8]). Different approaches to multi-objective single machine problems with fuzzy parameters have been presented in the literature during the last decade.
2. Job Shop Scheduling Problem (JSSP)
The job-shop scheduling problem, also known as the sequencing problem [5], is concerned with allocating limited resources to operations over time [9]. Although scheduling has an important role in the field of production and operations management, it is a difficult problem both theoretically and practically. Theoretical scheduling problems are related to the search for optimal schedules, subject to a limited number of constraints in a huge search space. These problems suffer from excessive combinatorial complexity. Practical scheduling problems are complex due to the number and variety of the constraints themselves, many of which are soft rather than hard physical constraints [10]. Informally, the job-shop scheduling problem can be described as follows. We are given n- jobs (Tasks) and m-machines (Processors). Each job consists of a sequence of operations that must be processed on m- machines in a given order. Each operation must be executed uninterrupted on a given machine for a given period of time and each machine can only handle at most one operation at a time. The problem is to find a schedule, an allocation of the operations of n- jobs to certain time intervals on m- machines, with minimum overall time [9,10].
3. Assumptions of Job-Shop Scheduling Problems (JSSP):
In a classical JSSP, n- jobs are processed on m-machines, in which the main assumptions are listed below: a) All jobs are available at time zero. b) Each job is processed by one machine at a time. c) A machine can process only one operation at a time. d) The processing times are fixed and sequence independent. e) The processing order of each job is given and fixed.
3.1 Indices and Parameters The following notations and definitions are used to describe the job-shop scheduling problem. n - Number of jobs m - Number of machines pi - Processing time of job, i (i=1,2,�n) di - Fuzzy Due Date of job, i (i=1,2,�n) μCP - Fuzzy Customer Priority μC - Fuzzy Membership function �Close� μD - Fuzzy Membership function �Distant� μsp - Sequencing Priority.
3.2 Decision Variables The fuzzy logic variables may have a membership value of not only o or 1 that is; the degrees of truth of a statement can range between 0 and 1 and is not constrained to the two truth values of classic propositional logic.
The fuzzy set theory [3, 11] is based on the extension of the classical definition of the set. In the classical set theory, each element of a universe X either belongs to a set A or not, whereas in the fuzzy set theory, an element belongs to a set A with a certain membership degree. Definition: A fuzzy set Ain X is defined by: A={( x,μ A(x))|x ∈X } where, μ A(x): X →[0,1] A μ is called the �Membership function� of A and μ A(x)is the �Degree of membership� to which x belongs to A.
4. Proposed Methodology:
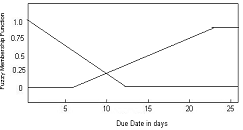
In this paper, the fuzzy methodology is applied to the scheduling of jobs; the objective is the determination of an optimal sequence for dynamic job arrivals such that potentially conflicting priorities are satisfied. The job-shop scheduling process includes the most important elements in many manufacturing areas such as: (A)Due Date (B) Customer Priority (C) Processing Time. A. Due Date (di) Due date is the number of days at any point, after which customer will arrive at the job shop expecting his job is completed. As per the usual method normally, the due dates is set as 28 days from the date of the order. The membership functions of �Closed� and �Distant� were assigned depending on the due date allocated. The fuzzy sets C = Close and D = Distant membership functions.
Hence given the universe U = [-∞, 28 days] � Z. Membership function can be defined as: Membership of �Close� Membership of �Distant� μc(x)=1.0x ≤ 0 μd (x) = 0 x ≤ 7 μc(x)=1.0-x/10 0< x<10 μd (x) = x/14 � 0.50 7 < x < 21 μc(x)=0 x ≥ 10 μd (x) = 1.0 21 ≤ x ≤ 28
The selection of a �trapezoidal� form of membership function for �close� is based on the assumption that the critically the closeness of an impending due date increases linearly with time up to the point at which the job is �late�. The �distant� function represents to avoid too early completion causing stock holding problem. B. Customer Priority (μCP)
The customer priority is based on the importance of a customer and based on the fuzzy values. The customer priority CP contains the five different fuzzy values. The customer priority fuzzy values are given below. Customer Priority (CP) = {Bad, Low, Medium, High, Very High}
C.Processing Time (pi) �Depending upon the processing time assigned to one particular job three fuzzy functions were assigned, for fuzzy set such as Short, Medium, and long�. It is the time required to process job (j) on any machine. The processing time (Pj), will normally include both actual processing time and set-up time. It is assumed that at the time of scheduling the exact processing times are unknown. a) Sequence Priority Rules (μsp) The sequencing priority is defined as: μsp(c, d) = Min {μc, μcp} ∨ Min{μcp, μd}, ..(2)
5. Exact Solution Flow Chart Approach:
� An Illustrative Example
Let us consider a single tailor machine job-shop Problem, where data about six pending jobs given in a single machine.
Table-1: Single Machine Six Jobs waiting to be processed.
Step-1 Lets Job 1: Calculate and compare the fuzzy value of �customer priority� with �close�, �distant�(As per mentioned flow chart steps). Min {μC, μCP) ∨Min {μCP, μD} *
(Min {1.0, 0.5} = 0.5)∨ (Min {0.5, 0.0} = 0.0) Max {0.5, 0.0} = 0.5 �Close� Thus: Medium and Close, Sequence: High. (According to sequencing priority rules). Similarly we can calculate the priorities values of other jobs as will, which are listed in Table 1 and from that, it is quite clear that Job 3 should be processes first, as it has the highest sequencing priority, is processed�duration 8 days. The sequencing priority comes out to be :3 > 1 > 4 > 5 > 2 >6.
Repeat all the tasks (Jobs) in step 1, for the remaining five jobs.
The current sequencing priority is given by: 1 > 2 > 6 > 4 > 5. Thus Job-1 is processed-duration 5 days. Similarly we draw tables and calculate sequence priority every time and after whole process, the final sequence priority (μsp) comes to be: Sequence Priority (μsp) = 3 >1 > 2 > 6 > 5 > 4. Three Piece Suit > Safari Suit > Repair Work > Ladies Suit> Shirt Trouser > Two Piece Suit.
Overall results can be summarized as:
The dynamic process can be summarized by considering the sequence priority each time the machine becomes available: 3 > 1 > 4 > 5 > 2 >6 �Job 3 be Processed 1 > 2 > 6 > 4 >5 � Job 1 be Processed 2 > 6 > 4 >5 � Job 2 be Processed 6 > 4 >5 � Job 6 be Processed 5 >4 � Job 5 be processed.
6. Concluding Remarks:
In this paper, a theoretical model has been presented which demonstrates how fuzzy decision making can support the dynamic scheduling process. With the objective to �Minimize the overall lateness (Tardiness)� and �Maximize the customer satisfaction� of the overall jobs has been formulated, and the optimal sequence for jobs with fuzzy due dates (di), fuzzy customer priority (Cp) and fuzzy Processing time (pi) has been determined. A real-world job-shop scheduling problem defined in tailor JSSP has been analyzed and solved using the proposed method and exact solution flow chart of (JSSP) approach. It is shown that the method is very flexible in different aspects and can be applied in treating real-life scheduling problems. It can be applied to a problem with any number of jobs, machines &objectives to be optimsed. Finally, the proposed method enables the DM to express performances regarding multiple objectives using natural language expressions and linguistic variables.
References:
[1] D.R. Sule, Industrial Scheduling, PWC Publishing Company, 1997. [2] R. Tavakkoli-Moghaddam, G. Moslehi, M. Vasei and A. Azaron, �Optimal Scheduling for a Single Machine to Minimize the Sum of Maximum Earliness and Tardiness Considering Idle Insert�, Applied Mathematics &Computation, Vol. 167, No. 2, pp. 1430-1450, 2005. [3] L.A Zadeh, Fuzzy sets,�Information and Control�,Vol. 8, pp. 338-353, 1965. [4] R.E. Bellman and L.A. Zadeh, �Decision Making in a Fuzzy Environment�, Management Sciences, Vol.17,pp. 141-164, 1970. [5] H.J. Zimmermann, �Description and Optimization of Fuzzy Systems�, International Journal of General Systems, Vol. 2, pp. 209-215, 1976. [6] H.J. Zimmermann, �Fuzzy Programming and Linear Programming with Several Objective Functions�, Fuzzy Sets and Systems, Vol. 1,pp. 45-56, 1978. [7] E.L. Hannan, �Linear Programming with Multiple Goals�, Fuzzy Sets & System, Vol.6,pp.235-164, 1981. [8] R.R. Yager, �Multiple Objective Decision-Making Using Fuzzy Sets�, International Journal of Man-Machine Studies, Vol. 9,pp. 375-382, 1977. [9] K. R. Baker, �Introduction to Sequencing and Scheduling�, New York: Wiley, 1974. [10] R. Bellman, A. Esogbue, and I. Nabeshima, �Mathematical Aspects of Scheduling and Applications�,Oxford, U.K.: Pergamon, 1982.
Author Biographies:
Dr.V.H.Bajaj Professor and Head Department of Statistics, Dr. B.A.M.University, Aurangabad (M.S.) India. He has guided more than 23 Ph.D. Students in the subject of Statistics, Computer Science. He has Published 55 Research Papers in various National and International Journals with impact factor and ISSN No. His areas of interests include Fuzzy Sets Theory and its Applications, Operations Research, Industrial Statistics, Data Mining and Data Warehousing, Data Envelopment Analysis.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||