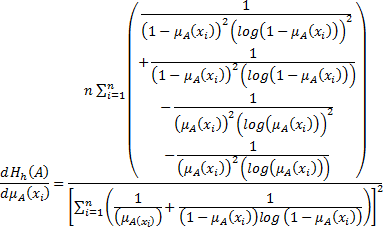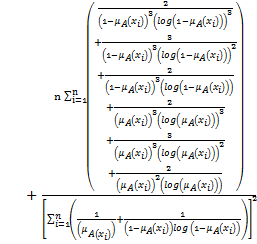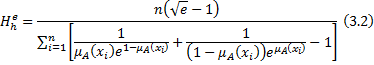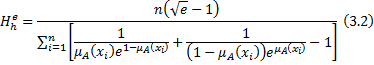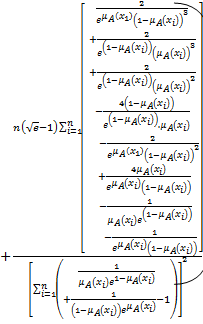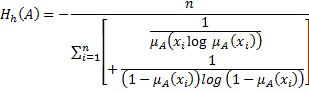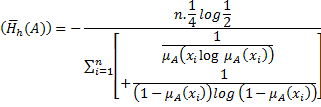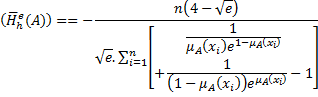|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Home| Journals | Statistics Online Expert | About Us | Contact Us | |||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| About this Journal | Table of Contents | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
[Abstract] [PDF] [HTML] [Linked References]
Harmonic Measures of Fuzzy Entropy and their Normalization
Priti Gupta1, Abhishek Sheoran2* 1,2 Department of Statistics, M.D. University, Rohtak, Haryana, INDIA. *Corresponding Address Research Article
Abstract: In the present communication, we give a brief summary about the various kinds of fuzziness measures investigated so far and formulate some critical aspect of the theory. Keeping in the view the non-probabilistic nature of the experiments, two new measures of fuzzy entropy have been introduced. The essential properties of these measures have been studied. The existing as well as the newly introduced measure of fuzzy entropy has been applied to the normalized principle. Keywords: Fuzzy Entropy, Crisp Set, Membership Function, Normalization.
Introduction The main concepts of information theory can be grasped by considering the most widespread means of human communication languages. Two important aspects of a concise language are as follows: First, the most common words (e.g., “a”, “the” and “I”) should be shorter than less common words (e.g., “Benefit”, “Generation” and “Mediocre”), so that sentences will not be too long. Such a tradeoff in word length is analogous to data compression and is the essential aspect of source coding. Second, if part of a sentence is unheard or misheard due to noise- e.g., a passing car- the listener should still is able to glean the meaning of the underlying message. Such robustness is as essential for an electronic communication system as it is for a language: properly building such robustness in to communication is done by channel coding. Source coding and channel coding are the fundamental concerns of information theory. Fundamental theorem of information theory state “It is possible to transmit information over a noisy channel at any rate less than channel coding with an arbitrary small probability of error.” Information theory considered here to be identified by Shannon (1948). Are probabilistic methods and statistical techniques be the best available tools for solving problems involving uncertainty? This question is often now being answered in the negative, especially by computer scientists and engineers. These respondents are motivated by the view that probability is inadequate for dealing with “certain kinds” of uncertainty. Thus alternatives are needed to fill the gap. Zadeh (1965) introduced fuzzy set as a mathematical construct in set theory with no intention of using it to enhance, complement or replace probability theory. Fuzzy sets plays a significant role in many deployed system because of their capability to model known statistical imprecision. A fuzzy set is a class of objects with continuum of grade of membership. Such a set is characterized by a member of functions which assign to each object a grade of membership ranging between 0 and 1. Fuzzy set A is represented as
Preliminaries Fuzzy Information Measures De Luca and Termini (1972) introduced the concept of fuzziness measure in order to obtain a global measure of the indefiniteness connected with the situations described by fuzzy sets. Such a measure characterizes the sharpness of the membership functions. It also can be regarded as entropy, in the sense, that it measures the uncertainty about the presence or absence of a certain property over the investigated set. They introduced a set of four axioms and these are widely accepted as criterion for defining any fuzzy entropy. In fuzzy set theory, the entropy is a measure of fuzziness which expresses the amount of average ambiguity or difficulty in making a decision whether an element belongs to a set or not. A measure of fuzziness P1 (Sharpness): P2 (Maximality): P3 (Resolution): P4 (Symmetry): Definition: A fuzzy set
The above defined properties are natural requirements for a measure of fuzziness. All measures introduced so far satisfy these properties. Since
In the next section, we discuss a brief summary about the various fuzziness measures investigated so far. The Survey of Some Existing Measures of Fuzzy Entropy This section includes various developments in the area of fuzzy information measures. Kaufmann (1975), proposed a measure using the generalized relative hamming distance as: And defined another measure using the generalized relative Euclidean distance as:
Ebanks (1983) defined fuzzy information measure for a fuzzy set as:
Kapur (1997) introduced the following measure of fuzzy entropy, which uses the Logarithmic scale as:
; α≥1, β≤1 After that Parkash and Sharma (2004) introduced two measures of fuzzy entropy, keeping in the view the existing probability measures, which are given by
; And
; Some other measure of fuzzy entropy were discussed, characterized and generalized by various authors. In next section, we put an effort to propose some new measure of fuzzy entropy corresponding to Harmonic Mean representation.
Measure of Fuzzy Entropy and their Validity Here, we introduced some fuzzy information entropy corresponding to harmonic mean, which are as follows: Fuzzy Entropy Corresponding to Harmonic Mean Firstly, we propose a new measure of fuzzy information as given by the following mathematical expression: 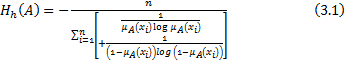 To prove that the measure
Hence,
Table 1
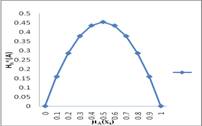
The value of
Figure 1: Graph Hh(A) Vs. µA(xi)
Exponential Fuzzy Entropy Corresponding to Harmonic Mean We propose here another measure of fuzzy entropy as follows:
Exponential Fuzzy Entropy Corresponding to Harmonic Mean We propose here another measure of fuzzy entropy as follows:
We shall prove that the measure introduced in equation
Proof: 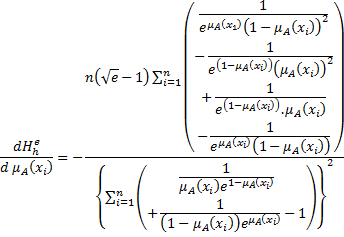
Also, 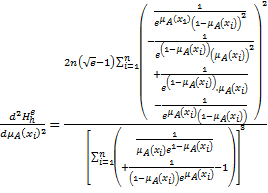
Since Hence,
1- 3. 4. 5. 6. Since
Table 2
The value of
Figure 2: Graph between
Normalized Fuzzy Information Entropy Need for Normalizing Fuzzy Information Measures The measure of fuzzy entropy due to De Luca and Termini (1.1) measures the degree of entropy among Example: let us consider the following fuzzy distribution,
Then, we have following fuzzy values for
We want to check which fuzzy distribution is more uniform or to which distribution the fuzzy values are more equal? From the values of two fuzzy entropies, it appears that B is more uniform than A, but still
For De Luca and termini’s [1] measure of fuzzy entropy, we have
Obviously, Thus, A is more uniform than B. This gives the correct result that B is less uniform than A. Thus, to compare the uniformity or equality or uncertainty of two fuzzy distributions, we should compare their normalized measures of fuzzy entropy.
Normalized Measure of Fuzzy Information Entropy In this section, we have proposed normalized measure of fuzzy entropy corresponding to,
The maximum value of above is given by
Thus, the expression for normalized measure is given by
Proceeding on the similar way, we can obtain the normalized measure of fuzzy entropy corresponding to [3.2] as:
On similar lines, we can obtain maximum values for different fuzzy entropies and consequently developed many other expressions for the normalized measure of fuzzy entropy.
Conclusion This work introduces two new measure of fuzzy entropy called fuzzy entropy corresponding to harmonic mean and exponential fuzzy entropy corresponding to harmonic mean. Some properties of these measures have been studied. We have also introduced the concept of normalized measure of fuzzy entropy is also introduced
References
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
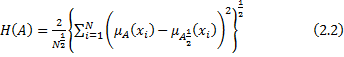
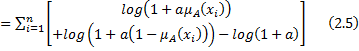
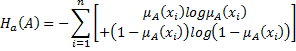
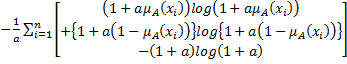 (2.6)
(2.6)