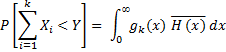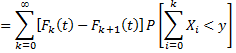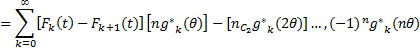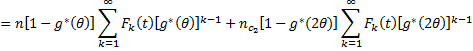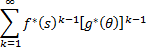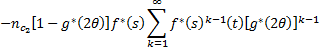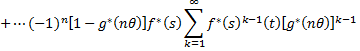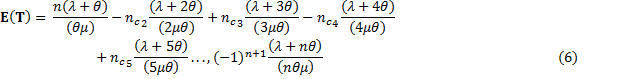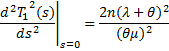• Thesis to Book with ISBN
• Aim And Scope
• Article in Press
• Editorial Board
• Current Issue
• Archives
• Publication Charges
• Authors Information
• Contact Us
• Paper Format

 [Abstract] [PDF] [HTML] [Linked References]

Determination of Expected Time to Seroconversion When the Antigenic Diversity Threshold Follows Order Statistic

R.M.Palanivel, P.Pandiyan and R.Sathiyamoorthi Department of Statistics, Annamalai University, Annamalai Nagar – 608 002 (TN) INDIA.

Corresponding Address:

[email protected]

Research Article

Abstract: In the study of HIV infection and consequent AIDS, the antigenic diversity is an important causative factor. A person, who has sexual contacts with an infected person, acquires more and more of HIV. This accentuates the increase in antigenic diversity of the invading antigen. When the total contribution to antigenic diversity on successive occasions of sexual contact crosses a particular level called the antigenic diversity, the seroconversion occurs. In this paper, the expected time to seroconversion and its variance are obtained under the assumption that the antigenic diversity is a random variable distributed as the nth order statistic. Numerical illustrations have also been provided.

Key Words: antigenic diversity thershold; seroconversion; nth order statistic.

Introduction:

The determination of the expected time to seroconversion is an important aspect in the study of HIV infection and its spread. When the cumulative antigenic diversity due to newly acquired HIV in successive contacts with an infected crosses a particular level called antigenic diversity threshold, the seroconversion occurs. The interarrival times between successive contacts are also random variables.

 The antigenic diversity threshold is taken to be random variable, since it differs from one individual to another. The concept of antigenic diversity threshold has been discussed by Nowak and May (1991).Kannan and Sathiyamoorthi (2008) have obtained expected time for the antigenic diversity of an infected individual to cross the threshold assuming that the antigenic diversity threshold is a random variable which follows exponential distribution. Ratchager et.al (2003) have considered a stochastic model for the estimation of expected time to seroconversion using the concept of order statistics. Palanivel et.al (2011) have estimated the expected time and its variance assuming that the antigenic diversity threshold is distributed as the first order statistic. In this paper the same concept is extended to the case when the threshold is distributed as nth order statistic. The shock model and cumulative damage process discussed by Esary et.al (1973) has been used in this model to estimate the expected time to seroconversion.

Assumptions of the model

The following are the assumptions used in this model

Notations:

Xi = a random variable denoting the contribution to the antigenic diversity, i =1,2… k and has p.d.f  g(.) with c.d.f  G(.).

Y = a random variable denoting the antigenic diversity threshold. It follows the nth order statistic, and has p.d.f  h(n)(.) and c.d .f H(n)(.)

Ui =  a random variable denoting the interarrival times between successive epochs of    exposure and has p.d. f (.) and c.d.f  F(.).

T = a random variable denoting the time to seroconversion with p.d.f  l(.) and c.d.f L(.)

Fk (.) =  k convolution of  F(.)

Results:

Let Y follows  nth order statistic

 and Let   

The probability that in k contacts during (0,t),the total antigenic  diversity generated does not exceed the threshold level Y is ,

                                                             (1)

           (2)

Where  denotes the probability of exactly k contacts during (0,t) by renewal theory.

                                                                               (3)

                                                                                                    On simplication

L (t) = P [T < t] = 1- S (t)                                                                                                                 (4)             Taking the Laplace trance form of L (t) we have L*(s) and then using the relationship

L*(s) =                

We have                                             

Now      

                                                                                                                                           (5)

  On Simplification

Then

Assuming that g (.) ~ exp (λ) and f(.) ~ exp (μ)

Now to find E (T2) we have

Now taking the terms T1 ,T2, T3, … Tn we have

          Now      V (T) = E (T2) – [E (T)] 2

From (6) and (7) the expression for V (T) can be obtained.

Conclusions:

• When λ which is the parameter of the random variable Xi, denoting the magnitude of contribution to antigenic diversity is on the increase, it is seen that E (T) increases. This is due to the fact that Xi follows exponential distribution and so E (Xi) = 1/λ. As λ increases then, 1/λ which is the contribution to antigenic diversity decreases. Hence it takes more time to cross the threshold. This is true when Y follows nth order statistic also. This has been shown in table (1) and figure (1).
•  The inter arrival times between successive contacts distributed as exponential with parameter μ. As μ increases, then E (U) = 1/μ decreases. Hence, the contacts will be more frequent and a greater contribution to the antigenic diversity. So, it takes less time to cross the threshold. Hence E (T) becomes smaller.  This has been indicated in table (2) and figure (2).
• The threshold is a random variable which is the nth order statistic. Now the threshold Y follows exponential with parameter θ. Hence E (y) = 1/θ and it decreases as θ increases.  Hence the threshold is smaller as θ increases. So as θ increases, it takes less time to cross the threshold as indicated in table (3) and figure (3).
• As ‘n’ increases, then the nth order also increases. This would mean that the magnitude of the nth order statistic will be greater. Hence, the threshold is higher and so it takes more time to cross the threshold and so E (T) is on the increase. This has been indicated in table (4) and figure (4).

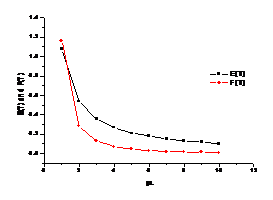
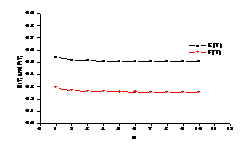
Table 1                                                                                                        Fig 1

θ=1.5 λ=1.2 n=10
μ	E (T)	V(T)
1	1.08	1.166
2	0.54	0.291
3	0.36	0.129
4	0.27	0.072
5	0.21	0.046
6	0.18	0.032
7	0.15	0.023
8	0.13	0.018
9	0.12	0.014
10	0.10	0.011



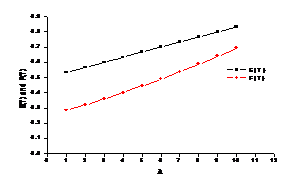
Table 2                                                                                                          Fig 2

 

θ=1.5                   μ=1.0                          n=10
λ	E (T)	V(T)
1	0.533	0.284
2	0.567	0.321
3	0.600	0.360
4	0.633	0.401
5	0.667	0.444
6	0.700	0.490
7	0.733	0.538
8	0.767	0.588
9	0.800	0.640
10	0.833	0.694



 

 

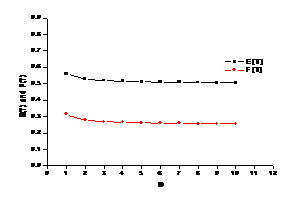
Table 3                                                                                                          Fig 3

λ=1.2 μ=1.0 n=10
Θ	E (T)	V(T)
1	0.560	0.314
2	0.530	0.281
3	0.520	0.270
4	0.515	0.265
5	0.512	0.262
6	0.510	0.260
7	0.509	0.259
8	0.508	0.258
9	0.507	0.257
10	0.506	0.256

 

 

                               






 

θ=1.5 μ=1.0 λ=1.2
n	E (T)	V(T)
1	0.540	0.292
2	0.520	0.270
3	0.513	0.264
4	0.510	0.260
5	0.508	0.258
6	0.507	0.257
7	0.506	0.256
8	0.505	0.255
9	0.504	0.254
10	0.504	0.254

 



 

 

Reference

1. Esary, J.D., Marshall. A.W., and Proschan.F, Shock Models and Wear   Processes, Ann.Probability, 627-649, 1973.
2. Nowak.M.A., and May.R.M., Mathematical biology of  HIV infections: Antigenic  variation and diversity threshold. Mathematical Biosciences, Vol.92, 201-229, 1991.
3. Sathiyamoorthi.R and Kannan.R., A Stochastic Model for Time to Seroconversion of   HIV Transmission, Journal of the Kerala Statistical Association, Vol.12, 23-28, 2001.
4. Palanivel.R.M., Pandiyan., Sathiyamoorthi.R., Estimation of Expected Time for Antigenic,2011
5. Diversity to Cross the   Threshold in HIV Infection. Proceeding of the National conference on  24th and 26th March, 2011, Manonmaniam Sundaranar University, Tirunelveli. Tamil Nadu.
6. Ratchager. N.P., Vijaya. S., Sathiyamoorthi. R. and Kannan. R., A stochastic model for estimation of time to seroconversion of HIV infected using order statistics. Proceedings of the National conference on Mathematical and Computational models, PSG college of Technology, Coimbatore, 37-42, 2003.