 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Home| Journals | Statistics Online Expert | About Us | Contact Us | ||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| About this Journal | Table of Contents | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
[Abstract] [PDF] [HTML] [Linked References] Hydromagnetic Oscillatory Flow through a Porous Channel in the Presence of Hall Current with Variable Suction and Permeability Khem Chand1 and Shavnam Sharma2 1Department of Mathematics & Statistics, H. P. University-Shimla (HP) INDIA. 2Research Scholar, Department of Mathematics and Statistics, H.P. University-Shimla (HP) INDIA. Corresponding Address: 1[email protected] , 2[email protected] Research Article
Abstract: An exact solution of hydromagnetic, oscillatory flow of an incompressible, electrically conducting and viscous fluid in horizontal porous channel embedded with porous medium of time dependent permeability is obtained in the presence of hall current. A magnetic field of uniform strength is applied along an axis perpendicular to the plane of the plate about which the entire system rotates. The effects of various parameters on the exact solution so obtained are discussed with the help of graphs and tables in detail. Mathematical Subject Classification: 76A05 Keywords: Hydromagnetic, oscillatory, rotating, porous medium, hall current.
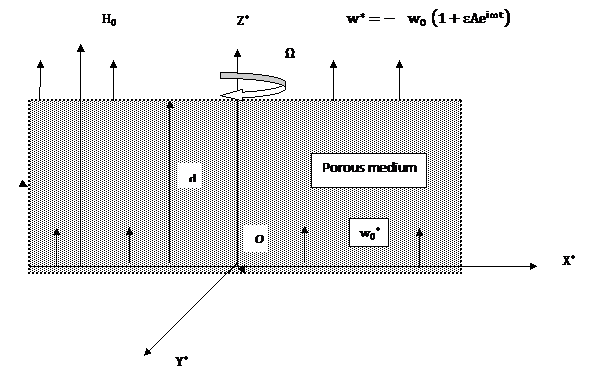
Introduction: Channels are frequently used in various applications in designing ventilating and heating of buildings, cooling electronic components, drying several types of agriculture products grain and food, and packed bed thermal storage. Convective flows in channels driven by temperature differences of boundary walls have been studied and reported, extensively in literature. On the other hand flows of fluid through porous medium are very important particularly in the fields of agriculture engineering for irrigation processes; in petroleum technology to study petroleum transport; in chemical engineering for filtration and purification processes. Abdussattar [1] and Ahmed [3] have studied free convection and mass transfer flow of a viscous fluid through porous medium. In most of these studied the permeability of the porous medium is assumed to be constant while the porosity of medium may not necessarily be constant because porous material containing the fluid is a non homogenous medium and there can be numerous in homogeneities present in a porous medium. Acharya et al [2] have analyzed free convection and mass transfer in steady flow through porous medium with constant suction in the presences of magnetic field. A number of investigation have been made by Raptis et al [9-11] into steady two –dimensional flow past a vertical walls of constant –permeability of porous medium. Notable among them are Attia and Kotb [4], Crammer and Pai[ 5], Ferraro and Plumpton [6], Shercliff [12] investigated a two-dimensional MHD flow between two porous parallel, insulated horizontal plates and the heat transfer through when the lower plate is kept stationary and upper plate is moving with uniform velocity. Singh et al [14] investigated a three –dimensional fluctuating flow through a porous medium when the permeability various both in time and space. Singh et al [13] have discussed hydromagnetic free convective and mass transfer flow of a viscous stratified fluid considering variation in permeability with direction. Further the flow of electrically conducting fluids in channel and pipes under the effect of transverse magnetic field occur in magnetohydrodynamic (MHD) generators, accelerators, pump and flow meters. In view of these and many others important applications of these types of flows a number of scholars have shown their interest. There are other industrial applications of flows of electrically conducting fluids in the fields of geothermal system, nuclear reactor, filtration etc, where the conducting fluid flows through porous medium which rotates about an axis. In view of the importance of rotating flows a number of studies appeared in literatures. Mazumder [8] studied an oscillatory Ekman boundary layer flow bounded by horizontal plates one of which oscillate and other is at rest. Singh and Kumar [15] studied an oscillatory MHD flow through a porous medium bounded by rotating porous channel in the presences of hall current by taking into consideration the constant suction and permeability. In this paper we present an investigation of the effect of magnetic field, hall current and rotation on a viscous incompressible and electrically conducting fluid in a porous horizontal channel filled with porous material by considering periodic suction and permeability. Mathematical Analysis: Consider an unsteady flow of an electrically conducting, viscous, incompressible fluid through a porous medium bounded between two insulated infinite parallel plates’ distances d apart. Choose the origin at the lower plate lying in The equation of continuity
Figure 1: The physical configuration of the problem Basic Equation: The equation of conservation of electric charge
Where For very large magnetic field, the
Since the external electric field arising due to polarization of charges is negligible. Hence
Thus within the frame work of these assumptions and making use of equation(4),the flow in the presence of Hall current by the following equations:
where The boundary conditions of the problem are The flow in presences of Hall current is governed by the following equations
Introducing the following non dimensional quantities
Eliminating the modified pressure gradient under the usual boundary layer approximation, equation (8) and (9) become
Using the non dimensional quantities the equation (10) and (11) become
The corresponding transformed boundary condition becomes
Equation (12) and (13) can be combined into a single equation by using the complex velocity of the form
The boundary conditions in complex notation is given by
Method of Solution:
Substituting (18) into (16) and comparing harmonic and non harmonic part we have
With corresponding transformed boundary condition
The solution of the equation (19) and (20) under the boundary condition (21) are obtained as:
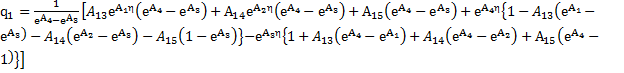 (23) (23)
Results and Discussion: Now for the resultant velocities and the shear stresses of the steady and unsteady flow, we write
The solution corresponds to the steady part which
The resultant velocity or amplitude and the phase differences of the unsteady flow are given by
The resultant velocities It is also found from figure 3 and 5 that the phase differences
2 1 10 0.2 0.2 I 4 1 10 0.2 0.2 II 2 3 10 0.2 0.2 III 2 1 20 0.2 0.2 IV 2 1 10 1 0.2 V 2 1 10 0.2 1 VI
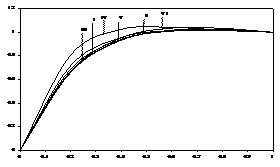
Figure 2: The Resultant velocity
2 1 10 0.2 0.2 I 4 1 10 0.2 0.2 II 2 3 10 0.2 0.2 III 2 1 20 0.2 0.2 IV 2 1 10 1 0.2 V 2 1 10 0.2 1 VI
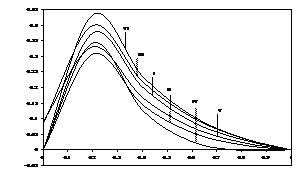
2 1 10 0.2 0.2 5 0.5 0.5 I 4 1 10 0.2 0.2 5 0.5 0.5 II 2 3 10 0.2 0.2 5 0.5 0.5 III 2 1 20 0.2 0.2 5 0.5 0.5 IV 2 1 10 1 0.2 5 0.5 0.5 V 2 1 10 0.2 1 5 0.5 0.5 VI 2 1 10 0.2 0.2 15 0.5 0.5 VII 2 1 10 0.2 0.2 5 0 0.5 VIII 2 1 10 0.2 0.2 5 0.5 0 IX

2 1 10 0.2 0.2 5 0.5 0.5 I 4 1 10 0.2 0.2 5 0.5 0.5 II 2 3 10 0.2 0.2 5 0.5 0.5 III 2 1 20 0.2 0.2 5 0.5 0.5 IV 2 1 10 1 0.2 5 0.5 0.5 V 2 1 10 0.2 1 5 0.5 0.5 VI 2 1 10 0.2 0.2 15 0.5 0.5 VII 2 1 10 0.2 0.2 5 0 0.5 VIII 2 1 10 0.2 0.2 5 0.5 0 IX

Figure 5: Phase angle For the steady flow the amplitude and the phase differences of shear stress at the stationary plate (
Here Table1: Amplitude
For the unsteady part of the flow the amplitude and the phase differences of the shear stresses at the stationary plate ( From figure 6 it is conclude that
2 1 10 0.2 0.2 0.5 0.5 I 4 1 10 0.2 0.2 0.5 0.5 II 2 3 10 0.2 0.2 0.5 0.5 III 2 1 20 0.2 0.2 0.5 0.5 IV 2 1 10 1 0.2 0.5 0.5 V 2 1 10 0.2 1 0.5 0.5 VI 2 1 10 0.2 0.2 0 0.5 VII 2 1 10 0.2 0.2 0.5 0 VIII
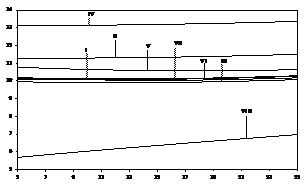
Figure 6: The amplitude
2 1 10 0.2 0.2 0.5 0.5 I 4 1 10 0.2 0.2 0.5 0.5 II 2 3 10 0.2 0.2 0.5 0.5 III 2 1 20 0.2 0.2 0.5 0.5 IV 2 1 10 1 0.2 0.5 0.5 V 2 1 10 0.2 1 0.5 0.5 VI 2 1 10 0.2 0.2 0 0.5 VII 2 1 10 0.2 0.2 0.5 0 VIII

Figure 7: Phase angle Concluding Remarks: The resultant velocities
References
Appendix
,
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
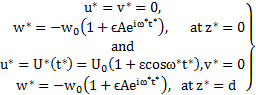
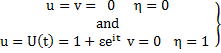 (14)
(14) 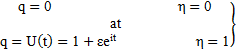 (17)
(17)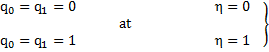 (21)
(21)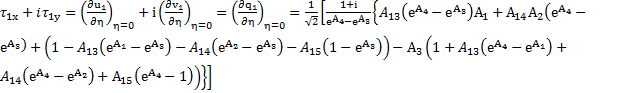 (30)
(30)