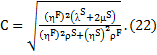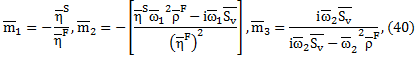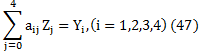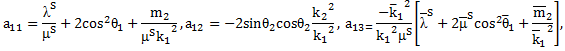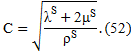|
||||||
|
|
Home| Journals | Statistics Online Expert | About Us | Contact Us | |||||
 |
||||||
| About this Journal | Table of Contents | ||||||
|
|
[Abstract] [PDF] [HTML] [Linked References]
Wave Propagation at a Loosely Bonded Interface between Two Fluids Saturated Incompressible Porous Solids
Neelam Kumari Assistant Professor, Department of Mathematics, Ch. Devi Lal University, Sirsa, 125055, INDIA. *Corresponding Address: Research Article
Abstract: Reflection and transmission phenomenon at a loosely bonded interface between two different fluid saturated porous half spaces is studied in the present investigation. P-wave or SV-wave incidents on the interface. The amplitude ratios for various reflected and transmitted waves to that of incident wave are obtained. After finding the amplitude ratios, they have been computed numerically for a specific model and plotted for different degree of bonding parameter. It is found that these amplitude ratios depend on angle of incidence of the incident wave and material properties of the considered medium and also these are affected by the bonding parameter. Also a special case is obtained and discussed from the present study accordingly. Keywords: Porous solid, reflection, transmission, longitudinal wave, transverse wave, amplitude ratios, empty porous solid.
Introduction Elastic waves propagation in fluid saturated porous medium has been studied for a long time due to its importance in various fields such as soil dynamics, hydrology, seismology, earthquake engineering and geophysics. Layers of porous solids, such as sandstone or limestone, saturated with oil or groundwater are often present in the earth’s crust. They are of great interest in geophysical exploration. Therefore the study of incompressible fluid saturated poroelastic solid in contact with another incompressible fluid saturated poroelastic solid is of great interest. Due to the different motions of the solid and liquid phases and different material properties and the complicated structures of pores, the mechanical behaviour of a fluid saturated porous medium is very complex. So many researchers tried to overcome this difficulty from time to time. Bowen (1980) and de Boer and Ehlers (1990a, 1990b) developed a theory for incompressible fluid saturated porous medium based on the work of Fillunger model (1913). For example, in the composition of soil both the solid constituents and liquid constituents are incompressible. Based on this theory, many researchers like de Boer and Liu(1994,1995), Kumar and Hundal (2003),de Boer and Didwania (2004), Tajuddin and Hussaini (2006),Kumar et.al.(2011) etc. studied some problems of wave propagation in fluid saturated porous media. In the problems of wave propagation at the interface between two elastic half spaces, the contact between them is normally assumed to be welded. However, in certain situations, there are reasons for expecting that bonding is not complete. Murty in 1975 discussed a theoretical model for reflection, transmission, and attenuation of elastic waves through a loosely bonded interface between two elastic solid half spaces by assuming that the interface behaves like a dislocation which preserves the continuity of stresses allowing a finite amount of slip. A similar situation occurs at the two different poroelastic solids, as the liquid present in the porous skeleton may cause the two media to be loosely bonded. Vashisth and Gogna (1993), Kumar and Miglani (1996), Kumar and Singh (1997) etc. discussed the problems of reflection and transmission at the loosely bonded interface between two half spaces. Using de Boer and Ehlers (1990) theory for fluid saturated porous medium, the reflection and transmission of longitudinal wave (P-wave) or transverse wave (SV-wave) at a loosely bonded interface between two different fluid saturated porous half spaces is investigated. A special case when fluid saturated porous half spaces reduce to empty porous solid half spaces has been deduced and discussed accordingly. Amplitudes ratios for various reflected and transmitted waves are computed for a particular model and depicted graphically.
Basic equations In 1990, de Boer and Ehlers described the governing equations for the deformation of an incompressible porous medium saturated with non-viscous fluid in the absence of body forces as
where In the case of isotropic permeability, to describe the coupled interaction between the solid and fluid, de Boer and Ehlers (1990) gave the tensor
where The displacement vector
and therefore equations (1)- (3) describing the equations of motion for fluid saturated incompressible porous medium in the component form can be written as
where
and
With the help of Helmholtz decomposition of displacement vector, the displacement components
Using, (16) in eqs. (9)- (13), we obtain the following equations:
where The normal and tangential stresses in the solid phase take the form,
Taking the time harmonic solution of the system of equations (17) - (21) as
where Using equation (25) in equations (17)-(21), we get
Equation (26) represents the propagation of a longitudinal wave with velocity and Using equations (27) and (28), we get
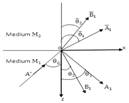
Equation (33) describes the propagation of transverse wave with velocity where Formulation of the Problem and its Solution. Consider a fluid saturated porous half space medium
Figure1: Geometry of the problem
In medium The potential functions satisfying the equations (17)-(21) can be taken as
where
and In medium The potential functions satisfying the equations (17)-(21) can be taken as follow
where and
Boundary Conditions The appropriate boundary conditions at the interface z=0 are the continuity of displacement and stresses. These boundary conditions can be expressed in the mathematical form as:
where
In order to satisfy the boundary conditions, the extension of the Snell’s law gives
Also
where
For P-wave,
For SV-wave,
For incident longitudinal wave at the interface z=0, putting
where
Also
For incident longitudinal wave (P-wave)
For incident transverse wave:
Special case: If pores are absent or gas is filled in the pores then
and the coefficients
and the remaining coefficients in (49) remain same. In this situation the problem reduces to the problem of empty porous solid half space over empty porous solid half space.
Numerical results and discussion In medium
In medium
Using MATLAB, a computer programme has been developed and modulus of amplitude ratios
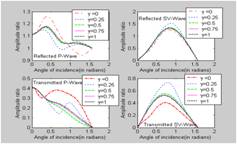
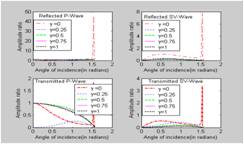
Incident P-wave Figures (2)-(5) show the variations of the amplitude ratios of reflected P-wave, reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of incident P-wave in general case of fluid saturated half spaces. The behaviour of all these distribution curves for reflected P-wave and for transmitted P-wave is similar i.e. they oscillate. For reflected SV–wave and transmitted SV-wave, the behaviour of all curves is also same i.e. increasing from normal incidence to maximum value and then decreasing from maximum value to grazing incidence. Figures (6)-(9) show the variations of the amplitude ratios of reflected P-wave, reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of incident P-wave in special case of empty porous solid half spaces. The effect of fluid filled in the pores of fluid saturated porous medium is clear by comparing the maximum values of corresponding amplitude ratio in figures (2)-(5) and (6)-(9). Also in these figures, the values corresponding to bonding parameter Incident SV-wave Figures (10)-(13) show the variations of the amplitude ratios for reflected P-wave, reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of the incident SV-wave whereas figures (14)-(17) represent the case of empty porous solid. The behaviour of all these curves in figures (6)-(9) and (14)-(17) is same i.e. they oscillates. In all the figures (10)-(17), the amplitude ratios for the bonding parameter
Figure 2-5: Variation of the amplitude ratios of reflected P-wave, reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of P-wave.
Figure 6-9: Variation of the amplitude ratios of reflected P-wave, reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of P-wave in case of empty porous solids.
Figure 10-13: Variation of the amplitude ratios of reflected P-wave, reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of SV-wave.
Figure 14-17: Variation of the amplitude ratios of reflected P-wave reflected SV-wave, transmitted P-wave and transmitted SV-wave with angle of incidence of P-wave in case of empty porous solids. Conclusion Numerical calculations are presented in detail for P-wave and SV-wave incident at the loosely bonded interface of considered model. For both the cases of incidence, it is observed the amplitudes ratios of various reflected and transmitted waves depend on the angle of incidence of the incident wave and material properties. The effect of fluid filled in the pores of incompressible fluid saturated porous medium is significant on amplitudes ratios. Effect of bonding parameter is significant on amplitude ratios. The research work is supposed to be useful in further studies; both theoretical and observational of wave propagation in more realistic models of fluid saturated porous solid present in the earth’s interior.
References
|
|||||
|
||||||