|
||
|
|
Home| Journals | Statistical Calculator | About Us | Contact Us | |
 |
||
| About this Journal | Table of Contents | ||
|
|
[Abstract] [PDF] [HTML] [Linked References]
Uses of Statistical Methodology in HIV/AIDS Projections Ramesh S. Patil1, Sajjan C.G.2 and Nagaraja Rao C3 1Lecturer/ Statistician, Department of Community Medicine, Navodaya Medical College, Raichur - 584101 2Lecturer, Veershaiva College, Bellary -583104 3Professor, Department of Statistics, Vijaya College, Bangalore-560004 Corresponding Adresses : Email: [email protected], [email protected], [email protected]
Research Article
Abstract: Projections of AIDS incidence are critical for assessing future health care needs. There is need for more accurate forecasts for the future course of the epidemic. Projections for the future of the epidemic have most often taken the form of trying to estimate how many new AIDS cases will be diagnosed (or reported) over some span of future years. Projections are very central for planning interventions and managing the available resources as they provide very valuable information on the number of undiagnosed infections. Issues that are necessary to the understanding and management of AIDS have generated several statistical challenges such as the choice of infection density, estimation of incubation period distribution, and dealing with sensitivity and studying of incomplete data. There were various mathematical and statistical approaches have been proposed to predict the future AIDS cases. In studying of AIDS, our main interest is in understanding the current situation and predicting the future path. Key words : HIV/AIDS, Time Series, Delphi survey method.
1. Introduction:
The first case of HIV infection in India was diagnosed among commercial sex workers in Chennai, Tamil Nadu, in 1986. Soon after, a number of screening centres were established throughout the country. Initially the focus was on screening foreigners, especially foreign students. Gradually, the focus moved on to screening blood banks. By early 1987, efforts were made up to set up a national network of HIV screening centres in major urban areas. A National AIDS Control Programme was launched in 1987 with the program activities covering surveillance, screening blood and blood products, and health education. In 1992 the National AIDS Control Organization (NACO) was established. NACO carries out India's National AIDS Programme, which includes the formulation of policy, prevention and control programmes.
Present Status of HIV/AIDS in India
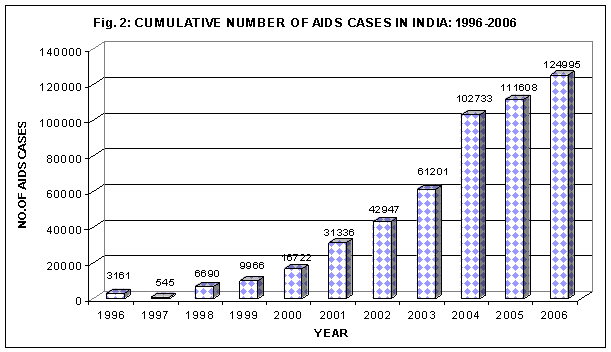
The estimates projected until recently were that globally India is leading over South Africa in terms of the overall number of people living with HIV. The United Nations Report on HIV released on Tuesday the 30th of May'06 said the World's second most populous nation has overtaken South Africa as the country with the most people living with HIV virus. India is home to about 5.7 million cases as against about 5.5 million cases infected in South Africa. � NACO estimated that the number of Indians living with HIV increased by 500,000 in 2003 to 5.7 million. Around 38 percent of these people were women. � By the end of May 2005, the total number of AIDS cases reported in India was 109,349 of whom 31,982 were women. These data also indicated that 37% of reported AIDS cases were diagnosed among people under 30. Many more AIDS cases go unreported. � The UN Population Division projects that India's adult HIV prevalence will peak at 1.9% in 2019. The UN estimates there were 2.7 million AIDS deaths in India between 1980 and 2000. During 2000-15, the UN has projected 12.3 million AIDS deaths and 49.5 million deaths during 2015-50. � A 2002 report by the CIA's (27) predicted 20 million to 25 million AIDS cases in India by 2010, more than any other country in the world.
The future of HIV/AIDS in India : There are many predictions about the effect that AIDS will have on India in the future and a lot of dispute about the accuracy of these estimates. Ruben del Prado, deputy UNAIDS country coordinator for India, has predicted that "there is going to be reversal of the epidemic by 2008 and 2009. This does not correlate with other UN-related estimates, however, which have suggested that:
Routes of HIV transmission :
AIDS is the most dreaded human misery with its impact felt in all over the world. It is a fatal transmissible disorder of the immune system that is affected by HIV. Slowly HIV attacks and destroys the immune system which is the body�s main defense against disease. HIV infects the defense cells of the immune system of the human body called CD4+ T lymphocytes and gradually reduces the cell number, thus, making an infected person defenseless and infections that eventually cause death. The end stage of HIV infection person is AIDS. At the end of incubation period of infected person, there is a rapid decrease in immune system which leads to an increase in sickness until death occurs. There are four basic modes of HIV transmission and they are: 1. Infected blood transfusion 2. Infected injecting equipments 3. Unprotected sex 4. Infected mother-to-child transmission HIV is transmitted through penetrative (anal or vaginal) and oral sex; blood transfusion; the sharing of contaminated needles in health care settings and through drug injection; and, between mother and infant, during pregnancy, childbirth and breastfeeding.
Treatment for HIV/AIDS :
Currently available drugs do not cure HIV infection but they do prevent the development of AIDS. They can stop the virus being made in the body and this stops the virus from damaging the immune system, but these drugs cannot eliminate HIV from the body. Infection with this virus results in the progressive deterioration of the immune system, leading to 'immune deficiency'. HIV is a very active virus that makes lots of copies of itself that then damage the body�s immune cells (CD4 cells). Taking the medicines everyday at the right time and in the right way keeps the right levels of the medicines in the body which makes it very hard for the virus to become resistant to the medicines. Current World Health Organization (WHO) recommendations for HIV treatment state that three separate ARV medicines need to be taken at all times. Some of these medicines can produce side effects such as nausea and vomiting or headaches. Usually most side effects are not serious and improve once the patient gets used to the medicines.
Understanding HIV/AIDS numbers :
In the beginning of public health surveillance for HIV/AIDS in Asia Pacific countries, no distinction was made between prevalent and cumulative numbers of HIV infection and/or AIDS. However, with time and the progression of HIV infection to AIDS and death, the constant widening difference between the prevalent number of HIV infection and the cumulative number became very obvious. As of the beginning of the new millennium, cumulative numbers of HIV infection and/or AIDS cases are not commonly used, except to put HIV/AIDS epidemics in this region into a historical perspective. Public health programmes now almost exclusively use prevalent and incident numbers. There is need a clear distinction to be made for each of the following types of HIV/ AIDS numbers � reported, official, estimated and actual. Official numbers of HIV/AIDS may be reported cases or, in some instances, may be officially estimated cases. Some care needs to be taken in evaluating estimated numbers since, depending on the data, assumptions and method(s) used to derive the estimate, the resultant figure can represent a reliable working estimate of the actual HIV/AIDS numbers or may represent gross overestimation or underestimation of these numbers. There were various mathematical and statistical approaches have been proposed to predict the future AIDS cases, numerous assumptions are required to account for the intrinsic and extrinsic dynamics of disease spread [1-3], and detailed models require specialized knowledge. This paper mainly describes the general methods used for estimations / projections of AIDS cases and reviews some statistical analysis of a few models which are developed for the estimation of AIDS cases recently. i. Application of various statistical methods in context of projection of AIDS cases. ii. Latest development in projection of AIDS cases.
2. Some Statistical Issues:
The statistical issues that arise concerning the statistics of the AIDS epidemic illustrate the impact of statistical forecasting in epidemiology. Analysis of studies of the epidemiology and natural history of infection with the HIV and subsequent onset of AIDS are complicated by many statistical issues. Several such problems are associated with the nature of data collection which is often unreliable and incomplete. In forecasting health care needs, [15] the number of patients at various stages of the illness and the rate of progression of AIDS will be a significant factor in public health planning. Our interest is in understanding the present state and predicting the future road. These are important concern to health care system, administrators, policy makers, epidemiologist and statisticians. Therefore, there is a need for quality information to be collected and analysed in an objective manner and presented in suitable format. Projections are very central for planning interventions and managing the available resources as they provide very valuable information on the number of undiagnosed infections. Issues that are necessary to the understanding and management of AIDS have generated several statistical challenges such as the choice of infection density, estimation of incubation period distribution, and dealing with sensitivity and studying of incomplete data. To answer the crucial questions, there must be an effective machinery to contribute to the available data among the researchers of different disciplines for their study purpose viz. 1. What is the period between infection and transmission? 2. How does the HIV transmissibility vary with time after got infection and with disease stage ? 3. What are the co-factors affecting infectivity? 4. What is responsible for the large variation in incubation time? 5. Will the current trend in the spread of HIV virus continue? 6. Can we able to explain the past growth of the epidemic? 7. Can we predict the future size of the epidemic accurately? To attempt the above questions, researchers need different types of data. Identifying the availability and sources of such data itself is the beginning. Statisticians have to evaluate the source of data available for prevalence and to develop estimation methods based on such data. The issues which are essential to understanding and management of the disease have generated numerous statistical challenges and which are as follows: i. Estimation of incubation period distribution ii. Projection of the course of the epidemic iii. Selecting proper infection density iv. Dealing with confidentially and analysis of incomplete data v. Inadequacy of data on HIV/AIDS for assessing the size and progression of epidemic. Today there is challenging role to play in the field of research of AIDS. They have responsibility about first to point out discrepancies in reported and actual numbers of HIV/AIDS counts. The big difference between reported and estimated numbers of HIV/AIDS counts in India, this is may be because of following reasons: i. Unreliable and inefficient reporting administration ii. Long and variable incubation period iii. For projection, use of improper methods iv. Allied sensitivity and social disgrace v. Insufficiency in the present AIDS surveillance data
Importance of AIDS cases :
Projections for the future of the epidemic have most often taken the form of trying to estimate how many new AIDS cases will be diagnosed (or reported) over some span of future years. In particular, we consider projection of the number of future cases, and estimation and identification of two key epidemiological unknowns, namely the properties of the incubation distribution and those of the infectivity associated with transmission. As data and projection methodologies improve, the differences in projections may be reduced for sub-Saharan Africa. [16] To provide a method for estimation and short-term projection of AIDS cases in areas where reporting of AIDS is unreliable. The method relies on estimation of annual HIV-infected "cohorts" and on annual progression rates from HIV infection to AIDS for each cohort. Estimation of annual infections is based on observations as to when HIV infections began to extensively spread and on the estimated shape and intensity of the annual infection curve. Using published and unpublished HIV serologic data, adult AIDS cases were estimated and projected for selected countries or regions in areas where homosexual men and IV drug users are the predominantly affected population (Pattern I); where heterosexual transmission of HIV predominates (Pattern II); and where HIV infection only began to spread extensively after the mid-1980s (Pattern III). This method is useful for estimating the current and future AIDS case load, especially in areas where the reporting of AIDS is unreliable. Such estimates are critically needed for public health and health care planning.
Due to large discrepancies between actual and estimated number of HIV/AIDS cases in India, there is a need for reliable projections, which are to be base on standard methodology which takes into account the transmission dynamics of the HIV. [14] Stress the need of accurate projections of the number of AIDS. If the projection methods are based not only on current incidence but also on the past incidence of HIV then it will helps us to know future path of the endemic better.
3. Methods for estimation/projection of HIV infection and AIDS cases:
In this section, we describes the limitations of the general methods used for estimating all the important and needed HIV/AIDS numbers including: prevalence, incidence and cumulative incidence of HIV infections, AIDS cases and AIDS deaths; and HIV-related diseases or conditions such as paediatric AIDS and maternal AIDS orphans and HIV-related tuberculosis cases. There has been an increasing need for estimates and projections in recent years for various purposes; monitoring and evaluating trends of incidence, etc.
Estimating HIV Incidence
Incidence estimates are more difficult to obtain than prevalence figures, but they are more informative about the effects of prevention efforts and the future of the epidemic. HIV incidence estimates can be obtained from: 1) observing seroconversions in a longitudinal study; 2) inferring incidence from serial cross-sectional surveys; 3) using capture-recapture methods in serial surveys; 4) back-calculation from reported AIDS cases; and 5) identifying recent seroconverters from a cross-sectional sample 6) using two HIV antibody tests of differing sensitivity for HIV antibodies.
The first method of estimating incidence is to enroll an HIV-negative population in a longitudinal, or cohort, study and to test the participants at regular intervals for new HIV infections, thereby deriving an incidence rate (number of new infections per total number of person-years of follow-up). Longitudinal studies with incident infections have been a valuable source of data.[6] Longitudinal studies are limited by the expense of conducting such a study, by the characteristics of the population enrolled, and the consideration that the longer the cohort is followed, the less likely it is that they are still representative of the population from which they were recruited.
The second method of estimating incidence is by conducting serial cross-sectional surveys in a population. This method does not directly estimate incidence, but incidence is indirectly estimated by the slope of the seroprevalence against time if the population being surveyed remains representative over time and if deaths and other losses to follow-up can be considered negligible. This approach has been suggested for estimating incidence from successive birth cohorts of recruits into the U.S. military.[7]
The third method is a variant on the cross-sectional survey approach that uses "capture-recapture," a methodology long used by biologists to study wildlife populations. It requires some sort of unique identifier, but not necessarily names, of individuals included in repeated surveys, so that the seroconverters among those repeatedly tested can be identified. This method was used to estimate incidence rates among injecting drug users in San Francisco by repeated testing in both clinic and street settings over a 5-year period while asking participants to receive their test results under a unique identifier constructed from the day of the month of their birth and their parents' first names.[8]
The fourth method uses "back calculation," which combines the available data on the numbers of reported AIDS cases and the incubation period distribution of AIDS (the mathematical function that estimates the probability of developing AIDS for each year following HIV infection) to derive how many HIV infections occurred during years past.[9] With information on past infections and AIDS cases, current HIV prevalence can be estimated. This technique requires fairly complete surveillance of AIDS cases and an accurate estimate of the incubation period distribution. It is limited by its inability to estimate HIV infections in recent years with any precision. More significantly, the large, and as yet largely unmodeled, effect of antiretroviral therapy on the incubation period has rendered back-calculation currently ineffective in estimating prevalence. The complexity of treatment regimens and their effects appear unlikely to be captured by an adjustment to the incubation distribution. For this reason, back calculation may no longer be a useful method of estimating HIV prevalence.
The fifth method is relatively new. It uses two HIV enzyme immunoassays: one is a current, highly sensitive test and the other has been made insensitive ("detuned"), in order to identify recent seroconverters from a single cross-sectional sample. As the quantity and avidity of antibody in peripheral blood increases progressively in the first weeks and months after HIV infection, a newly infected person will test positive on the sensitive assay and negative on the "detuned," as it is often called, or less sensitive assay. [10] One source of variation with this method is the viral subtype (clade) of HIV being tested. The average window of time captured by the two assays also needs to be determined and validated separately for assays of different manufacture. False positive seroconversions can occur in individuals with late-stage HIV infection, in which antibody levels decline, and in persons receiving antiretroviral treatment. Despite these limitations, this method has grown in use because it is the only method that allows an incidence estimate from a single cross-sectional sample. It is described by CDC as the serological testing algorithm for recent HIV seroconversion or STARHS.[11]
A sixth approach does not estimate HIV incidence per se but uses the number of reported AIDS cases in the youngest age range of adult cases, ages 13-25, as a surrogate for recent trends in incidence.[12] The justification for this approach is that onset of sexual and drug-using risk behavior in the teenage years (or later) leads to the inference that AIDS cases in this age group will be predominately those with a short incubation time from infection to AIDS and that therefore most of the cases reflect relatively recent infections (less than, say, 5 years on average).
Methods for estimating/projecting HIV prevalence:
1. Before the advent of effective drug therapy to prevent or delay the relentless progression from HIV infection to the development of AIDS, most of the developed countries considered that reported AIDS cases are to be sufficiently reliable for estimating/projecting HIV prevalence by using a back-calculation method. The back-calculation method used annual progression rates from HIV infection to AIDS and reported annual AIDS cases (usually after adjustments for delayed and incomplete reports) to calculate how many annual HIV infections would have been needed to generate the estimated/projected annual AIDS cases.
2. In the late 1980s and early 1990s to estimate HIV prevalence, there was use of �ratio� method that used an estimated ratio of prevalent HIV infections to prevalent AIDS cases. As the back-calculation method required reliable estimates of AIDS cases, in the same way, the ratio method also required reliable estimates of AIDS cases, which were usually not available. Apart from this, most users of the ratio method did not realize that in all HIV epidemics the ratio of prevalent HIV infection to prevalent AIDS cases changes rapidly over time. This HIV/AIDS ratio falls from many thousands to one during the first few years of an HIV epidemic, to less than ten to one after the first decade. This decline occurs whether HIV incidence is increasing or decreasing because, in the absence of effective treatment, virtually all HIV-infected individuals progress to AIDS. The HIV to AIDS case ratio is, therefore, almost all HIV and no or few AIDS cases.
3. An easy and useful method to estimate/project the current HIV prevalence in a �mature� HIV epidemic (one that has been in progress for about 10 years or longer) is to multiply by the estimated annual AIDS cases by 20. If the median period for HIV infection to the development of AIDS is assumed to be 10 years, then about 10 years after the start of an HIV epidemic, about 5% of prevalent HIV infections will develop AIDS on an annual basis. For example, if the estimated annual number of AIDS cases is 1000, then the estimated HIV prevalence would be about 20 000 (1000 multiplied by 20). Conversely, if HIV prevalence is estimated to be 20 000, then, by taking 5% of the HIV prevalence, one can calculate rapidly the expected annual number of AIDS cases to be about 1000. This is a �quick check and balance� method to see if the national estimate of HIV prevalence is compatible with the estimated annual number of AIDS cases or the reverse � if the estimated annual number of AIDS cases �matches� with the estimated national HIV prevalence.
4. In the absence of reliable AIDS case estimates or data, epidemiologists have estimated HIV prevalence by using the results of serological surveys and extrapolating these data to the total population of the age group 15-49 year. This has been and continues to be the primary method used in developing countries to estimate HIV prevalence. In this method, major problems are, the limited number of HIV seroprevalence studies that may be representative of specific populations or subgroups, and the wide variability in estimates of the size(s) of important HIV-risk behaviour groups or cohorts, viz. FSW, IDU and patients seen in STI clinics.
Estimation of HIV prevalence by using HIV serological data :
Using the available HIV serological data to derive a seroprevalence estimate, many epidemiologists have developed their own methods, assumptions and biases. Although HSS systems are not designed to provide data for making HIV prevalence estimates, they are widely used for this purpose, simply because there are usually no better serological data available. HIV prevalence in the 15-49 year-old population has been calculated according to the following general formulae: (1) The number of HIV infections in each of the major high-risk groups = the estimated number of the high-risk group (estimated for a specific population or a province) multiplied by estimated HIV seroprevalence rate (from HSS data); and (2) The number of HIV infections in the 15-49 year-old population = estimated HIV seroprevalence rate in antenatal women in the province (from HSS data) multiplied by the estimated number of 15-49 year-olds in the province (from census estimates).
Major sources of error:
1. Obviously error will occur while estimating HIV prevalence. The data quality and representativeness of the usual grab samples collected for most HSS systems can be seriously questioned. However, there have not been any systematic ways to quantify the probable range of error(s) related to such data quality issues. There has also been little effort to use the full range of data available, e,g. HIV prevalence from existing surveys, HIV prevalence in groups outside HSS, other data sources, etc. 2. Errors in estimating the size(s) of specific RBG can be quite large (up to several times higher or lower). 3. The probable heterogeneity of HIV risk within any specific RBG is well known, but frequently findings from sentinel HIV sites that tend to capture persons from those RBG with the highest or very high-risk behaviours are then extrapolated to the total RBG. This lead obviously will tend to higher HIV prevalence estimates. 4. In this method, a major assumption used is that HIV prevalence found in ANC can, with adjustment for the estimated male to female ratio, be used as a surrogate for HIV prevalence in the total 15-49 year-old population. However, this assumption has not been validated for other populations. 5. Measurement and/or estimation of the male to female (M:F) ratio of HIV infections has been carried out using a variety of methods and assumptions. In most of the epidemiological settings outside Africa (where there is a slight excess of infected females, compared with males) there has been a consistent and fairly large preponderance of infected males compared with females. 6. In heterosexual HIV epidemics in Africa, a marked urban-to-rural HIV differential, of up to 10-fold or more, was noted in the early phase of HIV spread. This differential narrowed markedly with time and after 10 years or more had been reduced to about 1-2-fold. One current assumption is that changes in the urban-to-rural HIV prevalence differentials in other developing country populations follow the same general course as that which has been observed in Africa. It is quite possible (and indeed probable) that, in other regions, heterosexual transmission of HIV may remain more localized in the highest RBG in urban centres and may penetrate or diffuse much more slowly (if at all) into most rural populations.
History of methods for projecting HIV Cases :
There is great uncertainty in projecting the future, especially for a complex problem such as HIV transmission. Even so, attempts to predict future trends and prevalence of HIV have been carried out with a very wide range of errors, using the following methods.
Delphi survey method :
The Delphi survey method was developed in an attempt to improve the reliability of the judgments needed in relatively uncertain situations, as well as to provide a means of quantifying such judgments. Essentially, the Delphi method obtains educated guesses from selected experts in a reiterative fashion, and then uses the average and range of the Delphi responses as projections. The main advantages of the Delphi method are speed and low cost. Though, it is difficult to select truly knowledgeable experts (i.e., experienced quantitative epidemiologists who are familiar with the epidemiology of HIV and general demographics of a specific country or population) to develop reliable estimates or projections of the number of HIV infections. This method should be used only for populations where no data are available.
Mathematical and computer/simulation models :
Mathematical and computer/simulation models have been used to develop short- and long-range projections of HIV prevalence. Yet, such models should be used primarily for hypothesis testing � not for making estimates and projections of the annual incidence/prevalence of HIV infection for a specific country or population(s). That was the conclusion of a United Kingdom expert committee that reviewed the situation in the United Kingdom in 1994. The committee concluded that the general uncertainty of many of the needed input parameters, such as the size of the risk groups, as well as reliable data on their current sex partner exchange rates, made estimation and projection of HIV/AIDS incidence and prevalence in the UK extremely uncertain. As a result, they stated clearly that model outputs should not be used for specific programme or policy development.
Method for short-term (less than 5 years) projection of AIDS cases/deaths:
A simple scenario/modelling approach for estimation and projection of AIDS cases was developed during the late 1980s by the Surveillance, Forecasting, and Impact Assessment (SFI) unit of the former WHO Global Programme on AIDS (GPA). This scenario/modelling approach or method can be used to provide working estimates and short-term projections of AIDS cases and deaths for policy development and public health planning. HIV/AIDS scenarios can be made up or constructed with or without models to �fit� the observed HIV/AIDS data and trends. The following is an outline of the general methods used in this scenario/modelling approach to develop working estimates and projections of HIV infections and AIDS cases and deaths.
(1) Assemble and analyse available HIV seroprevalence data to estimate the most recent pattern(s), prevalence and trends of HIV infection for a specific population. (2) Based on these data and other epidemiological observations, different HIV patterns and prevalence levels (i.e., scenarios) can be constructed with some confidence to the year 2005 for specific countries/populations. (3) An AIDS model can be used to derive annual and cumulative estimates and projection of AIDS cases/deaths and other HIV-related conditions, based on the general HIV scenario(s) constructed.
EPIMODEL :
EPIMODEL is a simple microcomputer programme developed by WHO in the late 1980s to estimate past and current prevalence, and to make short-term projections of AIDS cases and deaths in areas where AIDS case reporting was largely incomplete and unreliable. Most the problems encountered by users of EPIMODEL are associated with the quality of input parameters supplied by users. The basic module of EPIMODEL uses estimates of HIV prevalence and distributes this prevalence by annual HIV-infected cohorts back to the estimated start of the HIV epidemic along a selected epidemic curve. EPIMODEL then applies annual progression rates from HIV infection to the development of AIDS to each of the annual HIV cohorts to calculate annual numbers of adult AIDS cases and deaths. EPIMODEL provides default values for several input parameters that may be considered appropriate for modelling HIV/AIDS in a sub-Saharan African population, but all input parameters for EPIMODEL can be easily changed to better �fit� the specific population that is being modelled. It must be recognized that, in any large population, the spread of HIV infection and the subsequent appearance of AIDS cases is usually the consequence of several epidemics, i.e., in different �risk groups� or different geographical areas.
EPIMODEL was not designed to provide projection of HIV infection. The basic module of EPIMODEL was designed to estimate and project adult AIDS cases and deaths. This module can, with the additional input of a population denominator, calculate annual incidence and prevalence rates for HIV infection. Other modules of EPIMODEL include a Child module and Tuberculosis module. Aside from the potential errors described above, additional sources of potential error in using EPIMODEL include the following:
(1) One problem of EPIMODEL is in making only a single point of prevalence, with a starting year then generating a curve. Also, the greatest error could occur in estimating HIV point prevalence. Usually only subsets of data are used, representativeness of populations tested is not considered. (2) The �stage� of the HIV epidemic will have a significant impact on the estimates of annual HIV incidence and on estimates of annual deaths due to severe immune deficiency related to HIV infection. The stage and duration of the modelled HIV epidemic will also have a major impact on the estimated cumulative incidence of HIV infections and AIDS deaths. (3) Another possible source of error in producing estimates and projections of AIDS cases and deaths with EPIMODEL is the selection of the median interval period from HIV infection to death due to severe immunodeficiency related to HIV infection. The median interval from HIV infection to the development of severe immune deficiency appears to be similar in all populations (i.e., in developed and developing countries) and is estimated to be about 7-8 years. However, there is a consensus that the survival period from the development of severe immune deficiency to death is much shorter in most developing countries than in developed countries, where the advent of HAART therapy has significantly increased survival of patients with moderate immune deficiency related to their HIV infection.
The default median progression period from infection to AIDS in EPIMODEL is 10 years and the default median interval from AIDS to death for developing countries is less than 1 year. This has resulted in a median interval from HIV infection to death of 11 years. The change from this 11-year median survival period to the 9-year median progression period from infection to death results in much higher (up to 30% higher) cumulative numbers of HIV infections. In addition, use of a 9-year median survival period results in a higher (up to 60% higher) annual number of AIDS deaths.
Asian Epidemic Model (AEM) :
This model uses behavioral inputs to model HIV prevalence trends over time. This model has been able to fit 10 years of epidemiological and behavioral data in Thailand. The model contains six major population sub-groups: general population males and females, male clients of sex workers, direct and indirect sex workers, and injecting drug users. The size of each population and behavioural time trends (condom use, frequency of intercourse, etc.) will be determined from analysis of existing behavioural studies in the country. The transmission parameters (e.g. HIV transmission probabilities, STD cofactors, circumcision co-factors) will then be adjusted to fit to time trends in epidemiological HIV data in the country. This model will then produce estimates of new infections that would be more consistent with observed behavioural trends.
Time series analysis :
A time series is a chronological sequence of observations on a particular variable. The data points may be plotted to create a model, enabling one to quickly see trends, cycles, seasonal variations, or irregular fluctuations that occur over time. Once a pattern has been identified, it may be extrapolated into the future and used in forecasting [20]. In forecasting the AIDS endemic with time series analysis, then we have to pay attention to the following some questions: 1. How regular are the past HIV/AIDS trends? What are the chances that these patterns change? 2. Is future HIV/AIDS counts dependent at least partially on the present observable counts? 3. How reliable and accurate are the past data on HIV infection?
Future numbers of HIV/AIDS counts are necessarily based on the present incidence. However, question 1 and 2 are satisfactory answered, but question 3 is not. This happens due to sensivity factor associated with AIDS and lack of satisfactory diagnostic facilities which have led to large under reporting of AIDS cases. If the available data are corrected using a suitable method then they can be subjected to Time series analysis.
Extrapolation :
In the western area registration of AIDS cases are fairly complete and get reliable estimates of AIDS prevalence and incidence. Due to long asymptomatic period of infection and the fact that spread is mainly limited to specific exposure groups that are often difficult to contact, estimates of the prevalence and incidence of HIV infections cannot easily be obtained from registers of cases of HIV infection. However, [17] in some countries where AIDS registration is incomplete, HIV prevalence can only estimated by extrapolation from surveys. In this method the value of dependent variable x say, the number of AIDS cases is estimated for a given value of y, the independent variable, say the number of HIV seropositive or the number of persons exposed to risk of infection, which lie outside the existing range of y values. Newton-Gregory Forward interpolation formula is well-known one. In graphical approach, the fitted curve is extrapolated to a future time point. This classical method of extrapolation, which recognized a polynomial relation between x and y, is unlikely to be apply in the AIDS course in view of behaviour of AIDS data. So is the case with the multiple regression models. To choose the time period to model and the type of model to fit, it is important to identify changes in trends of AIDS incidence, especially in projecting AIDS cases by extrapolation. Because variations in the numbers of cases diagnosed from period to period can obscure changing trends, adjusted data on incidence were plotted with smoothed curves obtained from the lowness procedure [21]. Adjusted data on incidence, not the smoothed data, were used in back-calculation and extrapolation analyses.
A method to correct AIDS counts :
The method is briefly explained below, Define: nij : Number of New AIDS cases reported during the period I for the period of diagnosis j. where 1< j < I < t, where t being the number of periods under observation ( A period may be of 6 months duration ). It is considered that (i) nij are independently Poisson distributed with θij and (ii) all the reported casers are diagnosis correctly. Pk : Proportion of cases reported where k is the number of periods between diagnosis and report ; ∑ Pk = 1. n.j : Cumulative reported incidence for each period of diagnosis. N.j : Actual number of diagnosed AIDS cases which are not observable due to reporting delays. Here it is considered that every diagnosed case will be reported later or sooner. The parameter θij are then defined by, θij = N.j Pk with k = I � j, Pk > 0 3.921
Maximization of log likelihood of equation (3.921) results in the following equations: N.j = ∑ti=j nij / ∑t-j0 Pk, j= 1,2,3,�.t 3.922
Pk = ∑t-ki=1 ni+k.j / ∑t-ki=1 N.i k= 0,1,2,3,�.( t � 1 ) 3.923
Solutions of equations (3.922) and (3.923) can obtain using an iterative proportional fitting algorithm of [18]. It can be shown that equations (3.922) and (3.923) are conditional solutions to the problem of estimating the size of the multinomial population [19] and [5] have used similar estimators for the actual number of AIDS cases and subsequently fitted a line or curve by regression technique to the estimate.
Smoothing of Exponential trend :
Exponential smoothing was applied to several of the models in order to obtain clearer graphs for analysis. Exponential smoothing is a forecasting method that weights recent observations more heavily than remote observations. The equation for exponential smoothing is St = αyt + (1 - a)St-1 In this equation, St is the smoothed curve and α is the smoothing constant, which is always between zero and one. The trend inherent in HIV/AIDS data by moving average method can be improved by assigning the weights to each year reported AIDS case in geometric progression. Here greater weights are assigned to latest observations. Number of HIV positives can be taken as weights since the endemic is relatively young and there will be very few HIV positives in the very beginning of the spread than in recent years.
If the weights assigned are math version normal { 1, (1-ω), (1-ω)2, �..(1-ω)n-1 } to �n� observations ( 0 < ω < 1 ), then the weighted averages till the current year t and the succeeding year.
Taking n to be large, and higher powers of w and ( 1 � w ) and doing certain algebraic manipulations, the following relationship between xt+1 , the forecasting value for the next period and xt , the forecast value for the current period can be established.
i.e. the new forecast = [ω X observed value + (1-ω) X old forecast ]. Here xt+1 is the smoothed forecast, w is the smoothing coefficient and ( T- w/w ) is the trend factor. The forecast for the first period is generally taken from some old forecast if available or is often considered.
To minimizing forecast error: To attempt the situation in which the trend is upward but the forecast is low or conversely, a factor is added to make forecast value closer to the actual value. Equation (5.91) may be written as
Θt = [ w X change in smooth value ] + [ ( 1-w ) X proceeding trend coefficient ]
Then the forecast Ft is obtained by the relation, Ft = smoothed value + ( trend factor X trend coefficient ) And error of the forecast, Et =Xt - Ft The forecasts resulting from the single parameter exponential smoothing is consistently low because of there is an upward trend in the actual number of AIDS cases. To rise above of this, a second smoothing constant say the HIV seropositivity rate may be selected for trend itself.
While time series analysis was useful in gathering information about the population of HIV/AIDS patients as a whole, a second method, the multiple regression model, was used to examine HIV/AIDS mortality on an individual basis. We used the multiple regression method to build statistical models describing the dependence of the incubation period on a person�s age at HIV diagnosis and the chronological time since the start of the study. The Multiple Regression model uses more than one independent or predictor variable (denoted x1, x2, etc.) to explain dependent, or response, variable, y. The equation is shown here: y = �0 + �1 x1 + ߭2 x2 + ε
The two predictor variables, x1 and x2 , are a person�s age at the time of HIV contraction and the chronological time counting from the start of the study. These were used to explain the response variable, y, which is the length of time between a person�s contraction of HIV and their diagnosis of AIDS (the incubation period). �0 is the y-intercept. The error term, ε, explains the variation in the response variable that could occur given our combination of predictor variables.
Back-Calculation :
For long incubation period, this method is designed specially for AIDS cases. It is a method in which the number of AIDS cases can be projected from those already infected with the AIDS virus i.e. it reconstruct the past pattern of HIV infections and it is used widely to predict the number of AIDS cases apart from knowing the present situation [4]-[5]. Further, this projected can consider as the lower bound as this number will be expected even if there are no future infections. It preassumes the knowledge of incubation distribution among the infected that can develop AIDS. There is no need of assumption about the number of infected individuals or the probability of an infected individual eventually developing AIDS. Because of the long incubation period, this method does not account for further infection cases but can produce accurate short term projection. In this procedure, convolution equation namely, Z = X + T Where T is the variable denoting the length of incubation period, is the basis of the Back-calculation method. And X & Z are the random variables denoting the chorological times of infection and diagnosis for AIDS respectively. Let N denote the total number diagnosed upto the year L+1. Then, | |