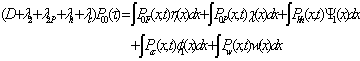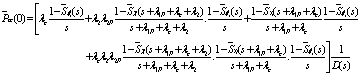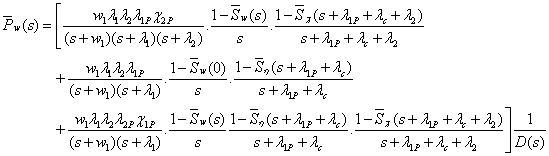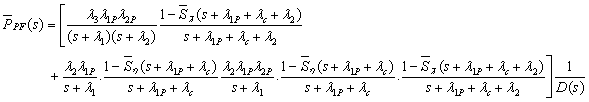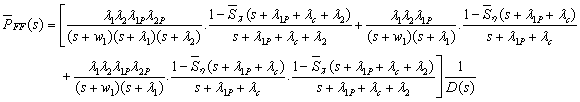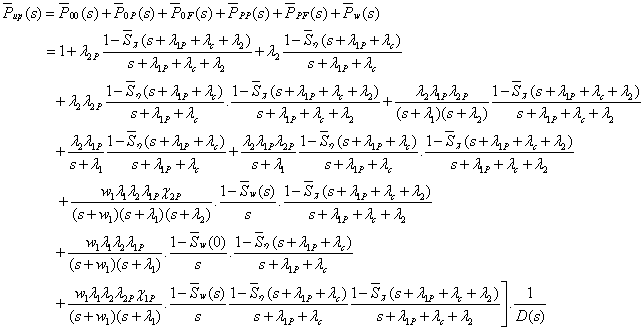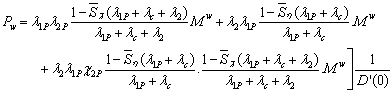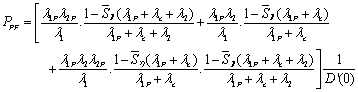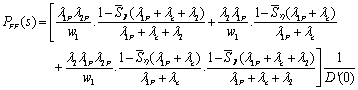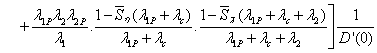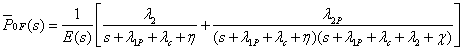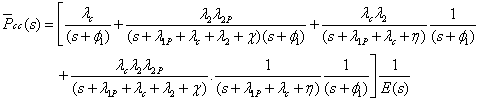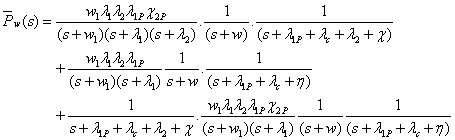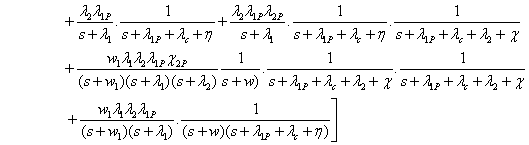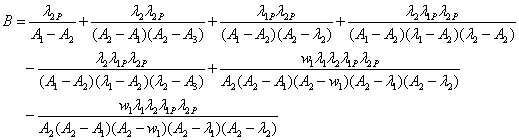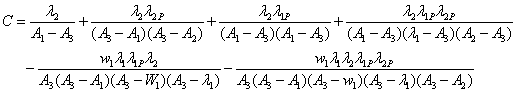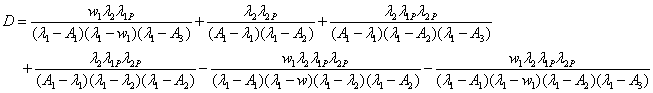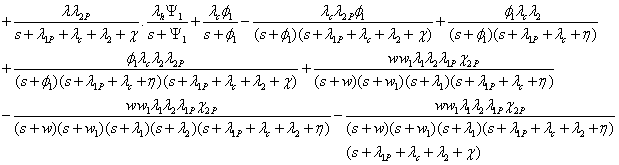|
||||||||||||||||||||||||||||||||||||||||||
|
|
Home| Journals | Statistical Calculator | About Us | Contact Us | |||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||
| About this Journal | Table of Contents | ||||||||||||||||||||||||||||||||||||||||||
|
|
[Abstract] [PDF] [HTML] [Linked References]
Reliability and Cost-Effectiveness of a Redundant System with Three Types of Failures and Repairs
Dharmvir Singh Vashisth1, A. S. Gousia Banu21Department of Mathematics, R.N. Engg. College, Rohtak (Haryana), INDIA. 2Department of Management, Narayana Engineering College (Nec) Nellore (A.P), INDIA Correspondence addresses [email protected] , [email protected] Research Article
Abstract:The goal of this paper is to carry out the reliability and cost effectiveness of a two unit cold standby system with allowed downtime and correlated failure and repair times. For this purpose, a stochastic Model is developed in which one unit is operative and other is kept as cold standby. Each unit has three modes of failure viz. normal, degraded and total failure. The time taken in replacement of a failed unit is negligible but it is a random variable. The failure rates are constant and system repair time are arbitrary distributed. The numerical results for reliability and cost-effectiveness are obtained using supplementary variable technique. The repair and failure times are correlated .
Introduction: In most of the reliability models of dissimilar units studied so far with three modes, viz, normal, partial and total failure have been considered. Gupta et al. [1] have studied two unit stand by system under partial failure and pre-emplive repair priority. They have all assumed that failure and repair are independent but it looks in practice that they have certain correspondence. Goel et al. [2] have considered that failure and repair time follow a behaviour exponential distribution. Sharma [4] has initiated the study of availability of the system which consist of two identical cold stand by units with constant failure rates. Initially one unit is operative while the other remains as stand by. Each of the units has three modes, i.e., normal, degraded and total failure. The system fails when both the units fail and may also fail due to common cause failure. The time taken in replacement of a failed unit by a stand by unit is not negligible but it is a random variable. Goel et al. [2] also presented a mathematical model for predicting a two identical active units redundant system with three types of failures namely mechanical, catastrophic and human failure. Any units may fail either partially or completely. And the system is only required when all the units fail including the helping unit. The failure rates are constant and system repair times are arbitrarily distributed. He obtained state probabilities by Laplace transforms. In this paper, we are interested to analyse the two unit cold stand by system with allowed downtime and correlated failure and repair times. Using this concept of correlation into consideration the joint distribution of failure and repair times is taken to be bivariate exponential distributed. The numerical results for reliability and cost-effectiveness are obtained to improve the importance of the study.
Notations:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
helping unit and
elapsed repair time lies in the interval
(h) failure of helping unit and elapsed repair time lies in the interval
(i)
elapsed repair
time lies in the interval
(j)
interval
(k)
repair time lies
in the interval
(l) helping unit)
(m) and complete failure of helping unit).
(n)
(o)
(p)
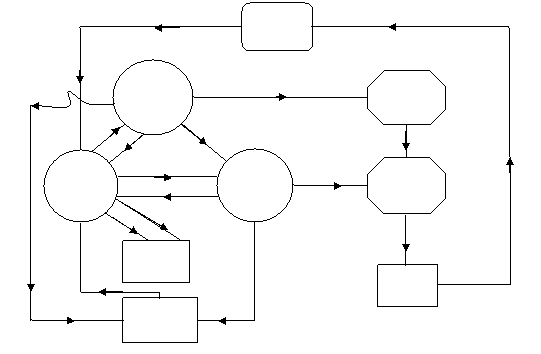
(q) Transition of diagram
Formulation of Mathematical Models:
Probabilistic consideration and preceding stated procedures yield the following equations:
Initial conditions
If a final state, it is ���..So
Mathematical Analysis:
Taking Laplace of the equation (2) we obtain
Gupta, Singh and Kishore [2] also obtained the
up and down state Probabilitie
Ergodic Behavior of the System:
Goel, Singh and Kishore [2] using base, we have
has obtained values as follows:
Also,
where,
Particular Cases:
(1) Constant Rate Repair: When repair rate is an exponential setting by
Goel, Singh and Kishore [2] the following value
Non Repairable System:
The Laplace system of transform of reliability when all repairs of the system are zero, i.e., given by
where,
The reliability of the system is
where,
Discussion:
We look parameters as follows as Goel, Singh and Kishore [2]. Let
The analyses for availability is obtained as follows:
(11)
Calculating values of
The values obtained above show that
Let us consider
On account of (12), (8) and (9), we get
R(t)
We draw a graph in R(t), i.e., reliability time. It is found that reliability decreases with time initially decreases is sharp but gradually it is a uniform decrease.
Cost Effectiveness of the system:
Assuming that the service facility is
always available and remains busy for time t during interval ] 0, t [.
Let
The profit function Profit(t)
Particular values of
.
Table : 1
This table shows the expected
profit during this interval (0, t) for the fixed value per unit of time.
This shows that expected profit v/s time decreases rapidly where service
cost References:
[1] Gupta P. P., Singh S. B. and Geol C. K., Stand by redundant system involving the concepts of multifailure human failure under head of line repair policy, Bulletin of Pure & Applied Sciences, 20, pp. 345-35, 2001. [2] Goel C. K., Singh S. B. and Jai Kishore, Reliability analysis of two units redundant system with three types of failure under waiting time to repair. Acta Ciencia Indica, XXIX,pp. 677-688, 2003. [3] Mokaddis G. S. and Tawfak M. L., Some characteristics of two dissimilar unit cold stand by redundant with three modes. Microelectron and Reliability, 38, pp. 487-504, 1996. [4] Sharma Viresh: Availability analysis of two unit by system with delayed replacement under perfect switching.
|
|||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||