|
On The Extension of Topological Local Groups with Local Cross Section
H. Sahleh1, A. Hosseini2
1,2Department of Mathematics, Faculty of Mathematical Sciences
University of Guilan, P.O.BOX 1914, Rasht – IRAN.
Corresponding Address:
[email protected] , [email protected]
Research Article
Abstract: In this paper, we introduce the cohomology of topological local groups and topological local extensions. We show that the second cohomology of a local topological group is in one to one correspondence with the class of topological local extensions with local cross sections.
keywords: Cohomology of topological local group, Strong homomorphism, Local cross-section, Topological local group extension.
MSC 2000: Primary 22A05, Secondary 22A10.
1.Introduction:
Let 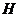 and and 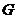 be topological groups, be topological groups, 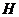 abelian. We consider abelian. We consider 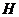 as a G-module with a continuous action of as a G-module with a continuous action of 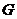 on on 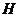 , that is, a continuous function from , that is, a continuous function from 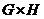 into into 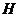 , carrying , carrying 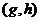 onto onto 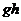 . .
By a topological extension of  by by 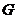 , , 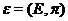 , we mean a short exact sequence , we mean a short exact sequence
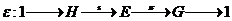 with with 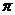 an open continuous homomorphism and an open continuous homomorphism and 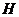 a closed normal subgroup of a closed normal subgroup of 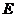 . .
Two extensions, 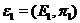 , and , and 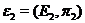 , of , of 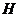 by by 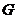 are said to be equivalent, are said to be equivalent, 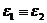 , if there exists a continuous isomorphism , if there exists a continuous isomorphism 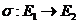 such that such that 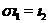 and and 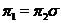 . The set of equivalence classes of extensions of . The set of equivalence classes of extensions of 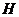 by by 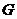 , denoted by , denoted by 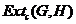 , with the Baire-sum is a group [2]. , with the Baire-sum is a group [2].
A cross-section of a topological group extension 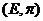 of of 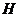 by by 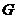 is a continuous map is a continuous map 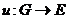 such that such that 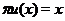 for each for each 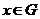 . There is a one to one correspondence between . There is a one to one correspondence between 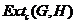 , and , and 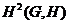 [2]. [2].
In this paper we show a similar result for topological local groups [3]. In section 1 we give some primarily definitions which will be needed in sequel. In section 2, we introduce the local extension on topological local groups and prove that the second cohomology of topological local group is isomorphic with the group of equivalence classes of topological local extensions with local crossed-sections.
We use the following notations:
• " 1 " is the identity element of  . .
• " " : " :  , , 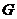 a sublocal group (subgroup) of a local group (group) a sublocal group (subgroup) of a local group (group) 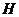 . .
•  where where  is a local group. is a local group.
2.Primary Definitions:
We recall the following definition from [5]:
A local group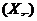 is like a group except that the action of group is not necessarily defined for all pairs of elements, The associative law takes the following form: if is like a group except that the action of group is not necessarily defined for all pairs of elements, The associative law takes the following form: if 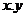 and and 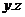 are defined, then if one of the products are defined, then if one of the products 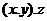 , , 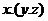 is defined, so is the other and the two products are equal. It is assumed that each element of is defined, so is the other and the two products are equal. It is assumed that each element of 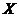 has an inverse. has an inverse.
Definition 2.1 [3] Let 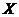 be a local group, if there exist: be a local group, if there exist:
- a distinguished element
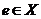 , the identity element, , the identity element,
- a continuous product map
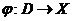 defined on an open subset defined on an open subset
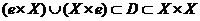 . .
- a continuous inversion map
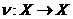
satisfying the following properties:
(i)Identity: 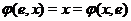 for every for every 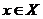
(ii) Inverse: 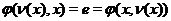 for every for every 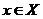
(iii) Associativity: If 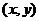 , , 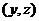 , , 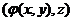 and and 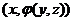 all belong to all belong to 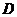 , then , then
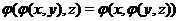
then 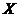 is called a topological local group. is called a topological local group.
Example 2.2Let  be a Hausdorff topological space and be a Hausdorff topological space and 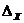 be the diagonal of be the diagonal of 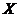 , , 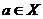 and and 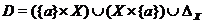 . Define . Define 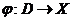 by: by:
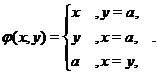
Now 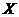 , by the action of , by the action of 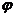 , is a local group. , is a local group.
If 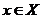 , ,  , we have , we have  . If . If  is a neighborhood of is a neighborhood of  , then , then  . There are two cases; . There are two cases;
 : since : since 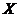 is Hausdorff, there are disjoint neighborhood is Hausdorff, there are disjoint neighborhood  , ,  containing containing  , ,  , respectively. Then , respectively. Then  and and  and and  . Hence, . Hence,  . So . So 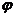 is continuous. is continuous.  : :  . .
If  and and  is a closed neighborhood of is a closed neighborhood of  in in 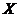 then then  . Hence, . Hence, 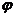 is continuous. Therefore, is continuous. Therefore, 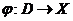 , ,  and and  , ,  are continuous. So are continuous. So 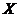 is a topological local group. is a topological local group.
Definition 2.3 Let 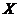 and and 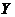 be topological local groups. We say that be topological local groups. We say that 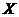 operates on the left of operates on the left of 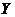 if: if:
There is a neighborhood 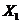 of the identity in of the identity in 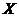 and a neighborhood and a neighborhood 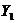 of the identity in of the identity in 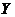 such that for every such that for every 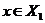 , , 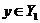 there exists there exists 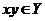 with the following condition: with the following condition:
1.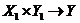 , , 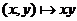 is continuous; is continuous;
2. 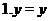 for all for all 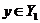 ; ;
3. If 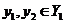 and and 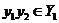 and and 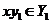 is defined for all is defined for all 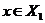 then then 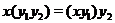 ; ;
4. If 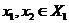 , , 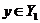 are so that are so that 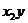 and and 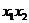 are defined in are defined in  and and 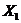 respectively, then respectively, then 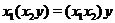 . .
Definition 2.4 A continuous map 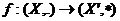 of topological local groups, is called a homomorphism if ; of topological local groups, is called a homomorphism if ;
1.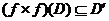 where where 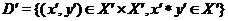 ; ;
2. 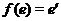 and and 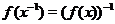 ; ;
3. if 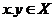 then then  exists in exists in  and and  . .
With these morphisms topological local groups form a category which contains the subcategory of topological groups.
Definition 2.5A homomorphism of topological local groups 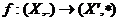 is called strong if for every is called strong if for every  , the existence of , the existence of  implies that implies that 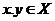 . .
A morphism is called a monomorphism (epimorphism) if it is injective (surjective).
Lemma 2.6 [1, Lemma 2.5] Let  be a symmetric neighborhood of the identity in a topological local group be a symmetric neighborhood of the identity in a topological local group 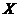 . There is a neighborhood . There is a neighborhood  of identity in of identity in  such that for every such that for every  , ,  . .
We denote the product of p copies of 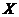 by by  . .
Definition 2.7Let 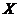 and and 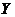 be topological local groups. A local p-map of be topological local groups. A local p-map of 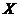 into into 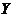 is a continuous map is a continuous map  where where  is a symmetric neighborhood of identity in is a symmetric neighborhood of identity in 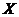 such that such that  whenever whenever  . .
Definition 2.8Let 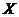 and and 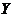 be topological local groups. Two local p-maps be topological local groups. Two local p-maps  and and  of of 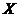 into into 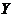 , where , where  are symmetric neighborhoods of the identity in are symmetric neighborhoods of the identity in 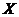 , are said to be equivalent if there is a neighborhood , are said to be equivalent if there is a neighborhood  with with  such that such that

whenever  for all for all  . .
Definition 2.9 The equivalence class of a local p-map is called a local p-cochain of 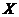 to to 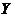 . .
Let 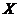 and and 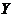 be topological local groups and be topological local groups and 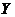 abelian (written additively). Let abelian (written additively). Let 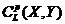 be the set of equivalence classes of local p-maps, with the usual addition of functions. The set be the set of equivalence classes of local p-maps, with the usual addition of functions. The set 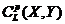 is an abelian group. Therefor, we define an addition on is an abelian group. Therefor, we define an addition on 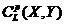 . Suppose . Suppose 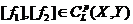 and and 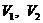 are symmetric neighborhoods of the identity in are symmetric neighborhoods of the identity in 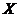 where where 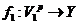 , , 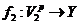 are local p-maps. Let are local p-maps. Let 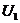 be a neighborhood of identity in be a neighborhood of identity in 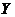 . By Lemma 2.6, there is a symmetric neighborhoods . By Lemma 2.6, there is a symmetric neighborhoods 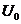 in in 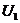 such that such that 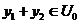 is defined when is defined when 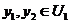 . Since . Since 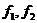 are continuous, then there exists a neighborhood are continuous, then there exists a neighborhood 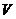 of 1 in of 1 in 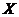 such that such that 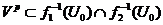 . Now define a local map . Now define a local map 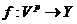 by by

for every 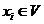 and and 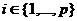 . It is clear that the local p-cochain . It is clear that the local p-cochain 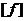 does not depend on the choice of the representations does not depend on the choice of the representations 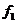 and and 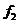 . Hence, we define an addition in . Hence, we define an addition in 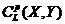 , by , by
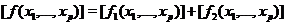 . .
Definition 2.10 Suppose 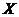 and and 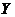 are topological local groups and are topological local groups and 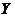 abelian. We define a coboundary operator abelian. We define a coboundary operator
 . .
Let 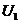 be a neighborhood of the identity in be a neighborhood of the identity in 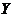 . By Lemma 2.6, there is a neighborhood . By Lemma 2.6, there is a neighborhood 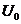 of the identity in of the identity in 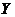 , ,  such that such that  is defined whenever is defined whenever  . Suppose . Suppose  is a neighborhood of 1 in is a neighborhood of 1 in 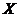 such that such that  whenever whenever  and and  . Suppose . Suppose  , ,  a local p-map. By continuity of a local p-map. By continuity of  , we choose a symmetric neighborhood , we choose a symmetric neighborhood  in in 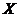 such that such that  . By Lemma 2.6, there is a symmetric neighborhood . By Lemma 2.6, there is a symmetric neighborhood  in in 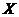 such that such that  , ,  for all for all  . .
Define a local (p+1)-map  , for each point , for each point  by by
 It is easy to show that the local (p+1)-cochain It is easy to show that the local (p+1)-cochain  depends only on the given local p-cochain depends only on the given local p-cochain 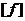 and and  . .
Definition 2.11 A local p-cochains 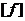 such that such that  is called a local p-cocycles. is called a local p-cocycles.
We denote the set of all p-cocyles by  . .
Definition 2.12 The image of a coboundry operator in  is called a local p-coboundry. We denote the set of all p-coboundries by is called a local p-coboundry. We denote the set of all p-coboundries by  . .
It is easy to show that  ,since ,since  . Then . Then  is a subgroup of is a subgroup of  . .
Definition 2.13 Let 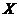 and and 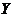 be topological local groups and be topological local groups and 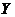 abelian. Then abelian. Then  is called the p-th cohomology topological local group. is called the p-th cohomology topological local group.
3.Second Cohomology and Topological Local Group Extensions:
In this part we prove that the second cohomology of a topological local group is isomorphic with the group of the equivalence classes of topological local extensions with local crossed-sections.
Definition 3.1 Let 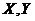 be topological local groups and be topological local groups and 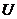 a symmetric neighborhood in a symmetric neighborhood in 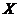 . The continuous map . The continuous map 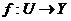 is an open continuous local homomorphism of is an open continuous local homomorphism of 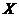 onto onto 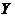 if if
1. there exists a symmetric neighborhood 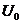 in in 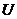 which which 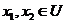 , , 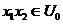 ; ;
2. 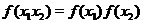 , , 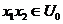 ; ;
3. for every symmetric neighborhood 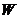 , , 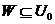 , , 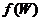 is open in is open in 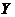 . .
The map 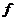 is called an open continuous local isomorphism of is called an open continuous local isomorphism of 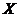 to to 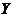 if if 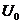 can be chosen that so can be chosen that so 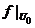 is one to one. is one to one.
Definition 3.2 A topological local group extension of the topological local group 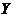 by a topological local group by a topological local group 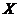 is a triple is a triple 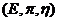 where where 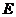 is a topological local group, is a topological local group, 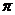 is an open continuous local homomorphism of is an open continuous local homomorphism of 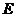 to to 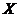 , and , and 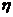 is an open continuous local isomorphism of is an open continuous local isomorphism of 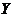 onto the kernel of onto the kernel of  [2]. [2].
Remark 3.3If 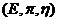 is a topological local group extension of is a topological local group extension of 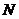 by by 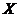 , where , where 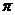 a strong homomorphism and a strong homomorphism and 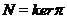 , then , then 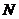 is a closed normal topological subgroup of is a closed normal topological subgroup of 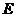 . .
Definition 3.4 Let 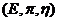 be a topological local group extension of be a topological local group extension of 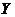 by by 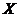 . A continuous map . A continuous map  where where  is a neighborhood of 1 in is a neighborhood of 1 in 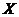 is called a local cross-section if is called a local cross-section if  for every for every  . .
Definition 3.5A topological local group extension 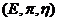 of of  is said to be fibered if it has a local cross section. is said to be fibered if it has a local cross section.
Definition 3.6A topological local group extension 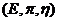 of of  is said to be essential if it has a local homomorphism of is said to be essential if it has a local homomorphism of 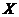 to to 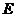 . .
Definition 3.7 Let  and and  be topological local extensions of an abelian topological local group be topological local extensions of an abelian topological local group  by a topological local group by a topological local group 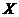 . If there exists a strong isomorphism . If there exists a strong isomorphism  of of  onto onto  such that such that  and and  . .

then and and  are equivalent, are equivalent,  . .
Note 3.8 Let 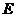 be a topological local group. The set be a topological local group. The set 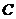 is called the center of is called the center of 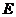 if if
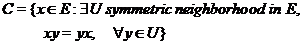 . .
In this paper, we replace 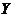 by by 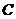 in Definition 3.2. In this case, in Definition 3.2. In this case, 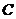 is a subset of is a subset of 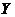 and and 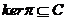 . .
Definition 3.9 Let 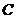 be an abelian topological local group. A pair factor set on topological local group be an abelian topological local group. A pair factor set on topological local group 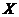 is a pair is a pair 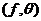 where where  is continuous, and is continuous, and 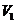 is a neighborhood of the identity in is a neighborhood of the identity in 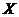 . Suppose there exist a neighborhoods . Suppose there exist a neighborhoods 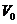 of the identity in of the identity in 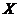 and and 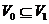 such that such that 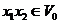 , for every , for every 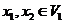 . Let . Let 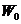 be a symmetric neighborhood in be a symmetric neighborhood in 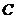 such that such that 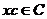 , for every , for every 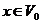 and and 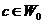 . .
Now, there is an action of 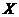 on on 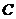 , , 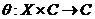 such that such that 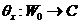 , for every , for every 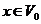 is a local inner automorphism, is a local inner automorphism,
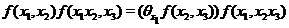 (3.1) (3.1)
whenever 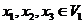 and and
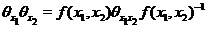 (3.2) (3.2)
for 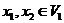 . .
Definition 3.10 The pair factor set 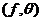 is normalized if is normalized if
 , ,  
where  is the identity automorphism. is the identity automorphism.
Remark 3.11Let  be an extension of be an extension of 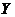 by by 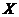 and and 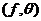 a pair factor set on a pair factor set on 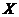 to to 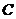 where where 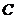 is locally isomorphism with the kernel is locally isomorphism with the kernel  . It is clear that . It is clear that  is a pair factor set on is a pair factor set on 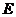 to to 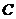 . We call . We call  the extension of the extension of 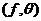 by by  . .
Let  be an extension of be an extension of 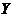 by by 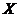 . The local cross-section . The local cross-section  of of  is called normalized if is called normalized if  . .
In this section we assume all pair factor sets and local cross-sections are normalized.
Definition 3.12 Let  be topological local groups. Suppose a topological local group extension be topological local groups. Suppose a topological local group extension  of of 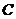 by by 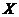 where where 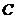 is locally isomorphism with the kernel is locally isomorphism with the kernel  with a local cross-section with a local cross-section  where where  is a neighborhood of the identity in is a neighborhood of the identity in 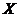 . There are a symmetric neighborhood . There are a symmetric neighborhood 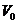 , ,  and a neighborhood and a neighborhood 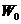 of the identity in of the identity in 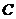 such that such that  and and  are defined for every are defined for every 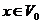 and and 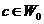 . Then, the action of . Then, the action of 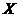 on on 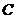 is defined by is defined by
 (3.3) (3.3)
In Definition 3.12, since 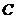 is the center of is the center of 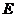 , we can easily see that for each , we can easily see that for each  and and  , the element , the element  dose not depend on the choice of the local cross-section dose not depend on the choice of the local cross-section . .
Proposition 3.13 Let 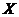 and and 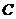 be topological local groups and be topological local groups and 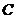 abelian. Suppose abelian. Suppose  is a topological local extension of is a topological local extension of 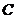 by by 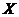 . Each local cross-section . Each local cross-section  of of  determines a pair factor set determines a pair factor set 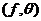 on on 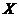 to to 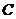 . .
Proof.Let 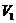 be a neighborhood of the identity in be a neighborhood of the identity in 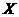 . By Lemma 2.6, there is a symmetric neighborhood . By Lemma 2.6, there is a symmetric neighborhood 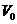 in in 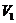 such that such that 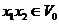 for all for all 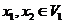 . Consider the continuous map . Consider the continuous map 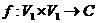 , ,  . Let . Let  and and  . Hence, . Hence,  and and  are defined in are defined in  . We define . We define


Let 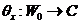 , ,  , where , where 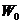 is a symmetric neighborhood and is a symmetric neighborhood and  . Then, . Then,  is a local automorphism. We show that is a local automorphism. We show that  is a pair factor set. We verify the first condition of Definition 3.9. Let is a pair factor set. We verify the first condition of Definition 3.9. Let  and and  and and  are defined in are defined in 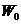 , since , since  and and  are in are in 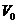 . Hence, the relation . Hence, the relation  implies that implies that
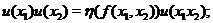
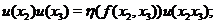
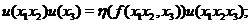
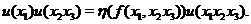
We have
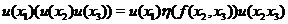
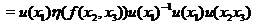
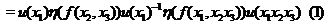 The right hand side of (1) is in The right hand side of (1) is in 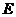 , since , since  , , 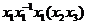 , and , and 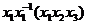 are defined in are defined in 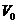 . Similarly, we obtain . Similarly, we obtain
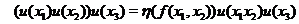
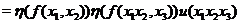 (2) (2)
By comparing (1) and (2),
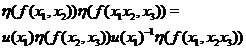
for 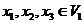 which proves (3.1). Now, for which proves (3.1). Now, for 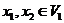 and and 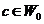 : :
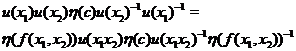 . .
So, (3.2) holds.□
Proposition 3.14 Let 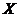 and and 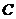 be topological local groups and be topological local groups and 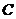 abelian. Suppose abelian. Suppose 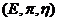 is a topological local extension of is a topological local extension of 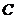 by by 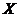 which has a continuous local cross-section which has a continuous local cross-section 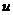 . Then, . Then, 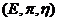 determines uniquely an element of determines uniquely an element of 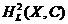 . .
Proof. Suppose 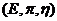 is a topological local extension with a local cross-section is a topological local extension with a local cross-section 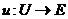 where where 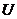 is a symmetric neighborhood of identity. Let is a symmetric neighborhood of identity. Let 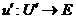 be another local cross-section of be another local cross-section of 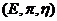 , , 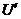 a symmetric neighborhood in a symmetric neighborhood in 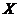 . Suppose the pair factor set . Suppose the pair factor set 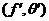 corresponds to corresponds to 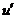 . .
We define a local cochain 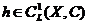 by by 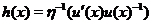 , for , for 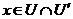 . .
By Lemma 2.6, there is a symmetric neighborhood 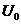 , , 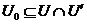 such that such that 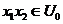 for for 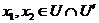 . The map . The map 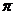 is continuous and by Lemma 2.6, there is a neighborhood is continuous and by Lemma 2.6, there is a neighborhood 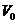 , , 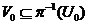 such that such that 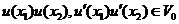 for for 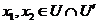 . .
Let 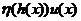 and and 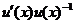 be defined in be defined in 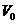 , ,  for all for all 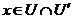 . Consider the continuous map . Consider the continuous map  , ,
 . .
 ; ;
 ; ;
 ; ;
by the action (3.3)

where  . Since . Since 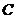 is abelian, then is abelian, then

 . .

Therefore, the pair factor set is independent of the choice of the continuous local cross-section.□
Definition 3.15 Let 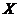 and and  be topological local groups with the action be topological local groups with the action 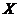 on on  . Suppose . Suppose  and and  are neighborhoods of the identities in are neighborhoods of the identities in 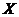 and and  respectively such that all products are defined . Let respectively such that all products are defined . Let  , ,  be a continuous strong homomorphism where be a continuous strong homomorphism where  and and  . We define . We define  by by

for every  and and  . The space . The space  is called the semi-direct product of topological local groups is called the semi-direct product of topological local groups 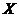 and and  with respect to with respect to  , denoted by , denoted by  . .
Proposition 3.16 Let 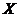 and and 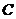 be topological local groups and be topological local groups and  abelian. Let abelian. Let  be a pair factor set on be a pair factor set on 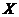 to to 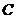 . There exists an extension . There exists an extension 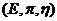 of of 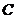 by by 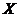 with a continuous local cross-section with a continuous local cross-section 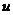 which corresponds to which corresponds to  . .
Proof. Let 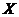 and and 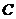 be topological local groups and be topological local groups and  abelian. Let abelian. Let  is a neighborhood of the identity in is a neighborhood of the identity in  . By Lemma 2.6, there is a symmetric neighborhood . By Lemma 2.6, there is a symmetric neighborhood  in in  such that such that  for all for all  . Suppose . Suppose  is a neighborhood of the identity in is a neighborhood of the identity in  . By Lemma 2.6, there is a symmetric neighborhood . By Lemma 2.6, there is a symmetric neighborhood  in in  , such that , such that  for all for all  . .
Suppose  . By [3, Theorem 2.28], . By [3, Theorem 2.28],  is a topological local group with the product is a topological local group with the product
 for every for every  and and  ; ;
where  is a local automorphism. is a local automorphism.
The identity of  is is  and the inverse is given by and the inverse is given by
 for for  and and  . .
The map  , ,  is a strong homomorphism, since is a strong homomorphism, since 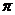 is the projection of is the projection of  onto onto 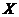 . It is clear that . It is clear that 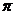 is open and continuous. The kernel is open and continuous. The kernel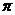 = =  consists of the elements consists of the elements  with the product with the product  whenever whenever  is defined. Since is defined. Since  is normalized then is normalized then  , for every , for every  . So . So  can be identified with can be identified with 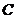 by the correspondence by the correspondence  . .
Let  . If . If  , we define , we define
 (3.4) (3.4)
We have




We can verify that
 (3.5) (3.5)




Then, by (3.4) and (3.5),  is a pair factor set of is a pair factor set of 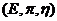 with the local cross-section with the local cross-section 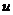 .□ .□
Remark 3.17Let  be a pair factor set of be a pair factor set of 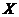 to to 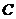 . By Propositions 3.13, 3.16, 3.14, every pair factor set corresponds to an element of . By Propositions 3.13, 3.16, 3.14, every pair factor set corresponds to an element of 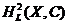 . Therefore, . Therefore,  determines determines  , ,  . Now, let . Now, let  , ,  be another local extension and be another local extension and  . .
By Proposition 3.13, there is a pair factor set 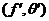 which corresponds to which corresponds to  . By Definition 3.7, choose an arbitrary open continuous strong isomorphism . By Definition 3.7, choose an arbitrary open continuous strong isomorphism  such that such that  and and  for for  . Then, . Then,  is a continuous local cross-section of is a continuous local cross-section of  . As in Proposition 3.14, . As in Proposition 3.14, 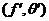 corresponding to corresponding to 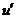 is identical with is identical with  corresponding to corresponding to 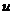 . Hence, equivalent local extensions of . Hence, equivalent local extensions of 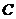 by by 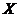 determine the same element of determine the same element of 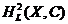 . .
Theorem 3.18 Let 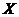 and and 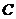 be topological local groups and be topological local groups and 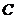 abelian. There is a one to one corresponding between the second cohomology of a topological local group abelian. There is a one to one corresponding between the second cohomology of a topological local group 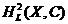 and the group of equivalence classes of topological local extensions with continuous local crossed-sections. and the group of equivalence classes of topological local extensions with continuous local crossed-sections.
Proof.By [4,Theorem 2.9], is a group. Then, it is immediate by, Propositions 3.13 and 3.16.□ is a group. Then, it is immediate by, Propositions 3.13 and 3.16.□
References:
- Goldbring, Hilbert's fifth problem for local groups, Annales. Math, Vol. 172, No.2, pp 1269-1314, 2010.
- S.T. Hu, Cohomology theory in Topological Groups, Michigan Math. J. Vol. 1, pp 11-59, 1952.
- H. Sahleh, A. Hosseini, A Note on topoogical local groups, Journal of Mathematical Sciences: Advances and Applications, Vol. 14, No .2, pp 101-127, 2012.
- H. Sahleh, A. Hosseini,The Group of Extensions of a Topological Local Group ,General Mathematics Notes (GMN), to appear.
S. Swierczkowski, Embedding Theorems for Local Analytic Groups, Acta . Math. Vol.114, pp 207-235, 1965.
|


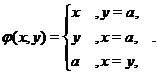
 It is easy to show that the local (p+1)-cochain
It is easy to show that the local (p+1)-cochain 
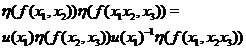
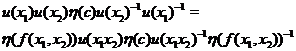 .
.  .
.