 |
||||||||||||||||||||||||||||||||||||
|
|
Home| Journals | Statistics Online Expert | About Us | Contact Us | |||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||
| About this Journal | Table of Contents | ||||||||||||||||||||||||||||||||||||
|
|
[Abstract] [PDF] [HTML] [Linked References] Squeeze Film Lubrication between Parallel Stepped Plates with Couplestress Fluids Biradar Kashinath Department of Mathematics, Government First Grade College, Shorapur, Dist: Yadgir, INDIA. Corresponding Address: Research Article Abstract: In this paper, a theoretical analysis of the effects of couple stresses on the squeeze film lubrication between parallel stepped plates is presented. The modified Reynolds type equation is derived on the basis of Stokes microcontinuum theory of couplestress fluids. The closed form solution is obtained. According to the results obtained, the influence of couple stresses enhances the squeeze film pressure, load carrying capacity and decreases the response time as compared to the classical Newtonian-lubricant case. The load carrying capacity decreases as the step height increases. Keywords: Squeeze film, Parallel stepped plates, couple stresses. 1 Introduction The squeeze film lubrication phenomenon is widely observed in several applications such as gears, bearings, machine tools, rolling elements and automotive engines. The squeeze film action is also seen during approach of faces of disc clutches under lubricated condition. The squeeze film phenomenon arises when the two lubricating surfaces move towards each other in the normal direction and generates a positive pressure and hence supports a load. This phenomenon arises from the fact that a viscous lubricant present between the two surfaces cannot be instantaneously squeezed out when the two surfaces moving towards each other and this action provides a cushioning effect in bearings. The squeeze film lubrication between two infinitely long parallel plates is studied by Cameron (1981). The flow of an incompressible fluid between two parallel plates due to normal motion of the plates is investigated by Bujurke. et al (1995). The unsteady flow between two parallel discs with arbitrary varying gap width was studied by Ishizawa (1996). The squeeze film with Newtonian lubricants has been studied by several investigators (Jackson, 1963; Burbidge and Colin servais, 2004; Gupta, 1977). The Rayleigh step-bearings with non-Newtonian fluids has been studied by many researchers (Hughes, 1963; Bujurke et al., 1987; Maiti, 1973; Elkouh and Yang, 1991). The use of different liquids as lubricants under different circumstances has gained its importance with a development of modern machines. In most of these lubricating oils the additives of high molecular weight polymers are present as a kind of viscosity index improvers. The presence of these additives in the lubricant prevents the viscosity variation of the lubricants with a change in temperature. The lubricants with additives causes the non-Newtonian behavior of the lubricating oils since the classical continuum mechanics of fluids neglects the size of fluid particles in the flow of fluids and hence several microcontinuum theories has been proposed to take into account of the intrinsic motion of material constituents(Ariman et al., 1973,1974). The Stokes (1966) microcontinuum theory of couplestress fluid accounts for the polar effects such as the couple stresses, body couples and asymmetric tensor. During last few decades Stokes microcontinuum theory has been extensively used to study the effect of couple stresses on the performance of various bearing systems viz: the slider bearings (Bujurke et al., 1990; Naduvinamani et al.,2003), Journal bearings (Mak and Conway, 1978; Guha, 2004), Squeeze film bearings (Lin, 1998; Naduvinamani et al., 2001) and thrust bearings (Ramesh and Dubey, 1975). These studies predicted the advantages of couple stress fluid lubricants over the Newtonian lubricants such as the increased load carrying capacity, decreased coefficient of friction in the slider bearings and delayed time of approach in squeeze film bearings. So far no attempt has been made to study the squeeze film characteristics with couplestress lubricants between flat stepped plates. Hence, in this chapter an attempt has been made to analyze the effect of couple stresses on these bearings. 2 Basic Equations The constitutive equations for force and couple stresses proposed by Stokes are
and where
and The dimensions of
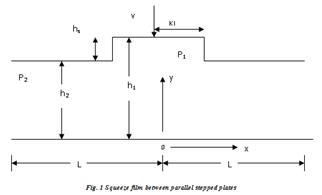
3 Mathematical formulation of the problem The squeeze film between parallel stepped plates approaching each other with a normal velocity V is shown in figure 1. The lubricant in the film region is considered to be an incompressible Stokes couple stress fluid. When body forces and body couples are absent, under the usual assumptions of hydrodynamic lubrication applicable to thin films the equations of motion (2.4) and (2.5) for the couple stress fluids in Cartesian coordinates take the form
The relevant boundary conditions are (i) At the upper surface y = h
(ii) At the bearing surface y = 0
4 Solution of the problem Solution of equation (3.1) subject to the boundary conditions (3.4a) and (3.5a) is
Where The volume flux of the lubricant is given by
where b is the width of the bearing. On using equation (4.1) in (4.2) gives
Where
Integration of the continuity equation (4.3) over the film thickness and the use of boundary conditions (3.4a) and (3.5a) gives
Integration of equation (4.4) w.r.t x and using the condition
The modified Reynolds type equation for determining the pressure is obtained from equations (4.3) and (4.5) in the form
where
The relevant boundary conditions for the pressure are
Solution of equation (4.6) subject to the boundary conditions (4.7a) and (4.7b) is
The load carrying capacity, W is obtained in the form
Which in nondimensional form
Where
Writing
Which in nondimensional form
Where
5 Results and Discussion This paper predicts the influence of couple stresses on the squeeze film characteristics of step bearings on the basis of Stokes couplestress fluid theory. The effect of couple stresses can be observed with the aid of nondimensional couplestress parameter 5.1 Load carrying capacity The variation of nondimensional load carrying capacity, 5.2 Time-height relationship The most important characteristics of the squeeze film bearings is the squeeze film time i.e. the time required for reducing the initial film thickness Table 1: Values of
6 Conclusions The squeeze film lubrication between parallel stepped bearings with couplestress fluid as lubricant is studied on the basis of Stokes microcontinuum theory for couplestress fluids. On the basis of the numerical computations of the results presented the following conclusions are drawn
In view of the above the squeeze film characteristics between parallel stepped plates can be improved by the use of lubricants with microstructure additives.
References
|
|||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
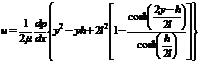 (4.1)
(4.1)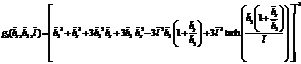 ,
,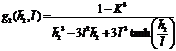 ,
,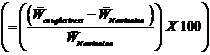 for different values of K is given in the table 1
for different values of K is given in the table 1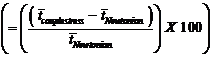 is given in the Table 1 for various values of
is given in the Table 1 for various values of 



