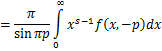|
||||||
|
|
Home| Journals | Statistics Online Expert | About Us | Contact Us | |||||
 |
||||||
| About this Journal | Table of Contents | ||||||
|
|
[Abstract] [PDF] [HTML] [Linked References] Applications of the Bi-Lateral Laplace-Mellin Integral Transform in the Range [0,0] to (¥,¥) Sarita Poonia1*, Rachana Mathur2 2Department of Mathematics, Govt. Dungar College, Bikaner, Rajasthan, INDIA. Corresponding Addresses: Research Article Abstract: In this paper we discuss Bi-Lateral Laplace-Mellin Integral Transform technique for solving initial value problem. This transform is studied in the range of [0,0] to ( Keywords: Laplace Transform, Finite Mellin Transform, Integral Transform, Double Bi Lateral Laplace Transform, Convolution and Parseval’s theorem
1.Introduction The Double Bi Lateral Laplace Transform is used to find the Bi-Lateral Laplace-Mellin Integral Transform in the range [0,0] to (
2.Preliminary Result The Double Bi-Lateral Laplace Integral Transform in Whenever this double integral exists and s > 0, p > 0 Substitute y = e-t , dy = - e-tdt , dy = -y dt and z = e-x ,dz = - e-xdx , dz = -z dx If t = -
Or Provided this double integral exists and s > 0 , p > 0 This is the Bi-Lateral Laplace-Mellin Integral Transform (BLLMIT) in the range [0,0] to ( It is denoted by
3. Result and Discussion 3.1. Properties 3.1.1: Linearity Property The BLLMIT is a linear operation theorem for the functions f(x,y) and g(x,y) and
then 3.1.2:Scaling Property The scaling property for BLLMIT in [0,0] to (
Then 3.1.3:Power Property The power property for BLLMIT in [0,0] to (
Then
3.2.Main Results 3.2.1:Inversion Theorem Assume that
then Proof If
and the Mellin Transform is
Then its inverse is
The BLLMIT in [0,0] to (
then
= = = = = By assuming This is the Inverse of Laplace–Mellin Integral Transform. It is denoted by
Or
3.2.2.Convolution Theorem The BLLMIT in [0,0] to (
Then
Proof The BLLMIT in [0,0] to (
= =
3.2.3:Parsavals Theorem The BLLMIT in [0,0] to (
Then
Proof The BLLMIT in [0,0] to (
= = =
3.2.4:Definitions (a) Unit Step Function :- If H(t) = U(t) = 1, when t > 0 = 0, when t < 0 Then H(t) = U(t) is known as the unit step function. (b) Heviside Unit Step Function If H(t-a) = U(t-a) = 1, when t > a = 0, when t < a Then H(t-a) = U(t-a) is known as the Heviside Unit Step Function. 3.2.5: First Shifting Theorem The BLLMIT in [0,0] to (
Proof The BLLMIT in [0,0] to (
= =
3.2.6:Second Shifting Theorem The BLLMIT in [0,0] to (
Proof The BLLMIT in [0,0] to (
Substitute x-c=u, dx=du , if x=0 then u=-c and if x=
Substitute x-c=u, dx=du , if x=0 then u=-c and if x=
3.2.7:Theorem ( Ramanujan’s Formula) If Then
Where This is the Laplace transform of f (x,-p) w.r.t. parameter s > 0 , denoted by L[f(x,-p),s] .
3.3.Derivatives Theorem: Suppose that 3.3.1: BLLMIT of first order partial derivative of The BLLMIT in [0,0] to (
By assuming Where
3.3.2: BLLMIT of second order partial derivative of
Where 3.4: Applications: The Cauchy’s linear Differential Equation is
The BLLMIT of
=
If
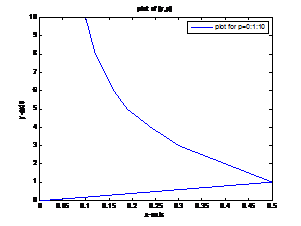
Where This is the required BLLMIT of Cauchy’s Linear Differential Equation. 3.5. Graphical Representation of BLLMIT of Cauchy’s Linear Differential Equation
Plot of (y,p): We consider 4. Conclusion: We have obtained interesting results of BLLMIT by using Ramanujan’s formula .To illustrate the advantages and use of these transforms, some important differential equation has been solved. We have also studied graphical representation of the solution using matlab.
References
|
|||||
|
||||||