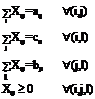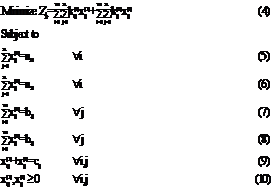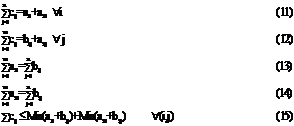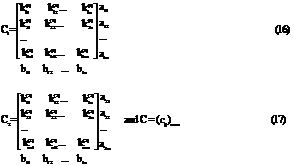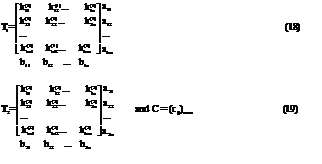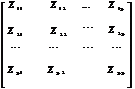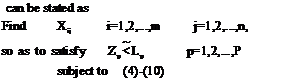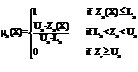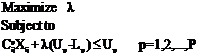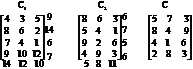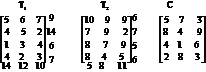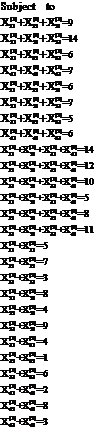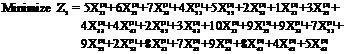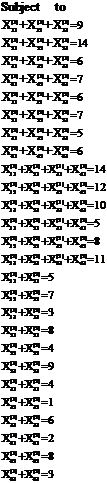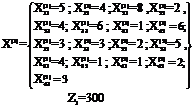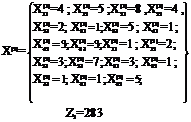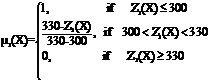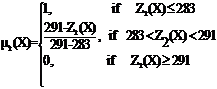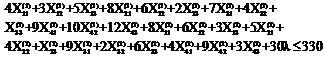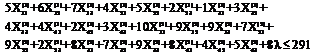• Thesis to Book with ISBN
• Aim And Scope
• Article in Press
• Editorial Board
• Current Issue
• Archives
• Publication Charges
• Authors Information
• Contact Us
• Paper Format

[Abstract] [PDF] [HTML] [Linked References]

Optimization Fuzzy Multi-Objective Multi-Index Transportation Problem with Linear Membership Function

M. H. Lohgaonkar

Dept. of Statistics, Shri Chhatrapati Shivaji Mahavidyalaya, Shrigonda, Ahmadnagar, Maharashtra, INDIA.

Corresponding Address:

[email protected]

Abstract: Fuzzy programming technique is used to solve multi-objective multi-index transportation problem in which objectives are conflicting in nature. The fuzzy programming method has been applied to find optimal compromise solution with the help of numerical example. 

Keywords: multi-Objective transportation problem, multi-Index transportation problem fuzzy linear membership function.

1. Introduction

            Fuzzy set theory was proposed by L. A. Zadeh (1965), and has been found extensive in various fields. Bellman and Zadeh (1970) were the first to consider the application of the fuzzy set theory in solving optimization problems in a fuzzy environment, these investigators constraints that both the objective function and the constraints that exist in the model could be represented by corresponding fuzzy set and should be treated in the same manner. The earliest application of it to transportation problems include Prade (1980), O’he’igeartaigh (1982), Chanas et al. (1984),Vedegay (1984) and Delgado et al. (1987). But these researcher emphases on investigating theory and algorithm. Furthermore, these above investigations are illustrated with simple instance slacking in actual cases of submission. On the other hand, these models are only of single objective and are classical two index transportation problems. In actual transportation problem, the multi-objective functions are generally considered, which includes average delivery time of the commodities, minimum cost, etc. The first attempt to fuzzify a linear programming with multiple objective functions was made by Zeleny (1973). Zimmermann (1978) applied the fuzzy set theory to the linear multicriteria decision making problem. It used the linear fuzzy membership function and presented the application of fuzzy linear vector maximum problem. He showed that solutions obtained by fuzzy linear programming always provide efficient solutions and also an optimal compromised solution. Aneja and Nair (1988) Showed that the problem model and Klingman and Phillips (1988) developed a model / solution procedure for adjusting to obtain an equitably infeasible solution for an infeasible solution for an infeasible transportation problem. Kligman and Phillips (1988) showed that the problem can be modeled and solved as a preemptive, multicritera, and capacitated transportation problem. Multi-index transportation problem are the extension of conventional transportation problems, and are appropriate for solving transportation problems with multiple supply points, multiple demand points as well as problems using diverse modes of   transportation demand or delivering different kinds of merchandises. Thus, the forwarded problem would be more complicated than conventional transportation problems. Junginger (1993) who proposed a set of logic problems, to solve multi-index transportation problems, has also conducted a detailed investigation regarding the characteristics of multi-index transportation problem model. Rautman et al. (1993) used multi-index transportation problem model to solve the shipping scheduling suggested that the employment of such transportation efficiency but also optimize the integral system. These references are only a single objective model and its constraints are not fuzzy numbers.

           In this study, a model is developed, and it combines fuzzy multi-objective programming and multi-index transportation problem to solve problem. This model cannot only satisfy more of the actual requirements of the integral system but is also more flexible than conventional transportation problems. Furthermore, it can offer more information to the decision maker (DM) for reference, and then it can raise the quality for decision-making. The fuzzy multi-objective multi-index transportation problem model is presented.

2. Mathematical Model

Multi-Objective Multi-index Transportation Problem

Let be multi-dimensional array  and let

 be multi-matrices then multi-index transportation problem is defined as follows

 (1)

Subject to

                     (2)

It is immediate that

  (3)

are three necessary conditions however they are noted to be non sufficient.

Multi-objective double transportation problem as follows

It may be easily seen that for existence of solution following set of conditions are necessary.

It may be easily seen that DTP is composed of two transportation tables and one C matrix as given below.

3. Fuzzy Algorithm to solve multi-objective multi-index transportation problem

Step 1:

Solve the multi-objective multi-index transportation problem as a single objective transportation problem P times by taking one of the objectives at a time

Step 2 :

From the results of step 1, determine the corresponding values for every objective at each solution derived. According to each solution and value for every objective, we can find pay-off matrix as follows

Where,  are the isolated optimal solutions of the P different transportation problems for P different objective functions  be the i-th row and j-th column element of the pay-off matrix.

Step 3:

From step 2, we find for each objective the worst (U_p) and the best (L_p)

values corresponding to the set of solutions, where,

    and    

An initial fuzzy model of the problem(4)-(10)

Step 4:  Case (i)

Define membership function for the p-th objective

function as follows:

              (20)

Step 5:

Find an equivalent crisp model by using a linear membership function for the initial fuzzy model

   (21)

Step 6: Solve the crisp model by an appropriate mathematical programming algorithm.

    (22)

4. Numerical Examples

Example 1

(27)

Example 2

 (28)

Example 1 is simplified as

  (29)

      (30)

Example 2 is simplified as

   (31)

             (32)

For objective , we find the optimal solution as

For objective , we find the optimal solution as

Now for  we can find out ,         

Now for  we can find out   

Pay-off matrix is

From this matrix 

 Define membership function for the objective functions and  respectively

   ;

Find an equivalent crisp model

 ,               and       

Solve the crisp model by using an appropriate mathematical algorithm.

    Subject to (30)

The optimal compromise solution of the problem is represented as

5. Conclusions

In this paper multi-objective multi-index transportation problem is defined and problem is solved by using fuzzy programming technique (Linear membership function).

References

1. Bit, A. K., Fuzzy programming with Hyperbolic membership functions for Multi-objective capacitated transportation problem, OPSEARCH 41 (2004) 106-120. 
2. Bit, A.K., Biswal, M.P., and Alam, S. S., Fuzzy programming approach to multi criteria Decision making transportation problem, Fuzzy sets and systems. 50 (1993) 135-141.
3. A.K. Bit, M.P. Biswal and S. S. Alam, Fuzzy programming approach to multi-objective solid transportation problem, Fuzzy sets and systems. 57 (1993) 183- 194.
4. Bit A. k., Biswal, M.P., and Alam S. S., Optimal planning for allocation of coal energy by goal programming, Industrial Engineering Journal XXII, No. 6 (1993) 8-12.
5. Haley, K. B., The solid transportation problem, Operations Research 10 (1963) 448-463.
6. Haley, K. B., The multi-index problem, Operations Research 11 (1963) 448-463.
7. Haley, K. B., The existence of a solution to the multi-index problem, Operations Research 16 (1965) 471-474.
8. Hannan E. L., Linear programming with multiple fuzzy goals, Fuzzy Sets and Systems.6 (1981) 235-248.