• Thesis to Book with ISBN
• Aim And Scope
• Article in Press
• Editorial Board
• Current Issue
• Archives
• Publication Charges
• Authors Information
• Contact Us
• Paper Format

[Abstract] [PDF] [HTML] [Linked References]

Visco-Elastic Free Convective Flow past a Vertical Porous Plate through a Porous Medium with Suction and Heat Source

Rita Choudhury¹, Saswati Purkayastha², Debasish Dey³

^{1, 2} Department of Mathematics, Gauhati University, Guwahati-781014, Assam, INDIA.

³ Department of Mathematics, Dibrugarh University, Dibrugarh-786004, Assam, INDIA.

Corresponding Addresses:

¹[email protected], ²[email protected], ³[email protected]

Abstract: The hydromagnetic free convective flow of a visco-elastic electrically conducting fluid past an infinite vertical porous plate in presence of constant suction and heat source has been analyzed. Approximate solution of the problem is obtained by using multi-parameter perturbation technique. The velocity field, temperature field, skin friction and rate of heat transfer are studied and the effects of visco-elastic parameter are illustrated with the combination of other flow parameters involved in the problem. The relevancy of this problem has been noticed in the fields of geophysics and astrophysics.

Keywords: Free convection, Heat source, Hydromagnetic flow, Porous medium, Suction.

1. Introduction

The mechanism of free convection has been attracted the interest of various researchers as it is highly used in many engineering applications such as designing, ventilating and heating of buildings, cooling electronic components, drying several types of agricultural products like grain,  food and packed bed thermal storage.  The consequences of free convection magnetic field under the application of transverse magnetic field have been used in the field of geophysics, astrophysics, engineering problems and in industrial purpose. Hasimoto [9] has studied the boundary layer growth on a flat plate with suction or injection. The effect of heat transfer on fluid flow with heat transfer along a plane wall has been explained by Gersten and Gross [8]. Soundalgekar [21] has discussed the free convection effects on steady MHD flow past a vertical porous plate. The flow behaviour of hydro-magnetic free convection past an accelerated vertical plate has been investigated by Raptis and Singh [15]. An analysis of unsteady hydro-magnetic free convection flow with constant heat flux has been done by Singh and Sacheti [19] by using finite difference scheme. Jha [10] has investigated the effects of applied magnetic field on transient free convective flow in a vertical channel. The nature of unsteady free convective MHD flow with heat transfer past a semi-infinite vertical porous moving plate with variable suction has been analysed by Kim [11]. Sharma and Pareek [18] have studied the free convective flow past a vertical porous moving surface in presence of transverse magnetic field. The combined effects of heat and mass transfer in MHD flow of a viscous fluid past a vertical plate under oscillatory suction velocity have been explained by Singh et al. [20]. Makinde et al. [12] have investigated the unsteady free convection flow with suction on an accelerating porous plate. The impact of constant suction and heat sink on unsteady free convective MHD flow past an infinite vertical plate has been analysed by Sahoo et al. [16].  Sarangi and Jose [17] have examined the flow behaviour of unsteady free convection and mass transfer past a vertical porous plate and variable temperature in presence of transverse magnetic field. The effect of variable suction on unsteady magneto-hydrodynamic flow past an infinite vertical moving plate in presence of heat transfer has been explained by Ogulu and Prakash [14]. Das et al. [5] have studied  the mass transfer effects on unsteady flow past an accelerated vertical porous plate with suction numerically. The flow pattern of unsteady free convection past an accelerated vertical plate with suction and heat flux in presence of transverse magnetic field has been analysed numerically by Das et al. [6].  A theoretical explanation on unsteady free convective MHD flow past a vertical porous plate through a porous medium with suction and heat source has been given by Das et al. [7]. Nowadays, researchers have shown their interest in the area of non-Newtonain fluid flow field as these are used in geo-physics, chemical engineering (absorption, filtration), petroleum engineering, hydrology, soil-physics, bio-physics, paper and pulp technology. Mansutti  et al. [13] have examined the steady flows of non-Newtonian fluids past a porous plate with suction or injection. Choudhury and Dey [2,3], Choudhury and Mahanta [4] Choudhury and Debnath[1] etc. have analysed a number of problems for flows past a flat plate under different physical situations. In this study, an analysis is carried out to study the hydro-magnetic free convective flow of a visco-elastic fluid past an infinite vertical porous plate through a porous medium in presence of constant suction and heat source. The velocity field and the shearing stress at the plate are obtained and illustrated graphically to observe the visco-elastic effects in combination with other flow parameters.

The constitutive equation for Walters liquid (Model B^/) is

 ,  

where  is the stress tensor, is isotropic pressure,  is the metric tensor of a fixed co-ordinate system is the velocity vector, the contravarient form of  is given by

It is the convected derivative of the deformation rate tensor  defined by

Here is the limiting viscosity at the small rate of shear which is given by

N( ) being the relaxation spectrum . This idealized model is a valid approximation of Walters liquid (Model B¢) taking very short memories into account so that terms involving

  ,                          (1.5)                                 

have been neglected.

Walters [22] reported that the mixture of polymethyl metha crylate and pyridine at 25⁰ C containing 30.5 gm of polymer per litre and having density 0.98 gm/ml fits very nearly to this model. Polymers are used in the manufacture of space crafts, aeroplanes, tyres, belt conveyers, ropes, cushions, seats, foams, plastic, engineering equipments, contact lens etc. Walters liquid (Model B^/) forms the basis for the manufacture of many such important and useful products.

Consider the unsteady free convective flow of a viscous incompressible electrically conducting fluid past an infinite vertical porous plate in presence of constant suction and heat flux and transverse magnetic field. Let the x´-axis be taken in vertically upward direction along the plate and y´-axis normal to it. Neglecting the induced magnetic field and the Joulean heat dissipation and applying Boussinesq’s approximation the governing equations of the flow field are given by:   

Continuity equation

Momentum equation

Energy equation

The boundary conditions of the problem are:

We now introduce the following  non-dimensional quantities :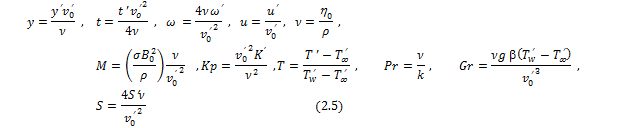

where  g is the acceleration due to gravity, ρ is the density, s is the electrical conductivity, ν is the coefficient of kinematic viscosity, b is the volumetric coefficient of expansion for heat transfer , ω is the angular frequency,  is the coefficient of viscosity, k is the thermal diffusivity, Τ is the temperature ,  is the temperature at the plate,   is the temperature at infinity, Pr is the Prandtl number, Gr is the Grashof number for heat transfer, S is the heat source parameter, Kp is the permeability parameter and M is the magnetic parameter.

The non-dimensional form of (2.2) and (2.3) are as follows:

The corresponding boundary conditions are:

3. Method of solution

To solve equations (2.6) and (2.7), we assume e to be very small and the velocity and temperature in the neighbourhood of the plate as

Substituting equations (3.1) and (3.2) in equations (2.6) and (2.7) respectively, equating the harmonic and non harmonic terms and neglecting the coefficients of  , we get

Zeroth order equations:

subject to boundary conditions are :

First order equations :

with relevant boundary conditions are,

Using multi-parameter perturbation technique and taking K<< 1, we assume

Now using equations (3.9), (3.10) in equations (3.3) and (3.6) and equating the coefficients of like powers of K and neglecting the higher power of K, we get the following set of differential equations:

Zeroth order :

The modified boundary conditions are:

First order:

The corresponding boundary conditions are,

Solving equations (2.12) and (2.15) subject to the boundary conditions (2.13) and (2.16), we get

Also solving equations (3.11), (3.12) subject to the boundary conditions (3.13) and solving (3.14), (3.15) subject to the boundary conditions (3.16), we get

with the use of above solutions, the velocity and temperature fields are expressed by

3.1. Skin Friction

Figure 1: Variation of transient velocity u against y for Pr=5, S=0.2, Kp=4, M=1, ω=5.0, ωt=π/2, ε=0.01

The effects of Grashof number on velocity profile are obtained from figure 1. Grashof number (Gr) characterizes the free convection parameter for heat transfer and is defined as the ratio of buoyancy force to the viscous force. In our study, we have considered the positive values of Grashof number. Gr > 0, interprets that flow past an externally cooled plate. The figure states that rising value of Grashof number declines the viscosity of both Newtonian and non-Newtonian fluids, which in turn boost up the speeds of both the fluids.

Figure 2: Variation of transient velocity u against y for Gr=7, S=0.2, Kp=4, M=1, ω=5.0, ωt=π/2,ε =0.01

In fluid flow problems, the significance of Prandtl number cannot be ignored, as it studies the simultaneous behaviour of both momentum and thermal diffusions. Figure 2 represents the effect of Prandtl number on velocity profile. Prandtl number is defined as the ratio of momentum diffusion to thermal diffusion. The rising value of Prandtl number raises the thickness of the fluid and hence the fluid experiences a decelerating trend. This physical phenomenon is observed in Newtonian as well as visco-elastic fluid.

Figure 3: Variation of transient velocity u against y for Gr=7, Pr=5,  Kp=4, M=1,  ω=5.0, ωt=π/2, ε=0.01

Figure 4: Variation of transient velocity u against y for Gr=7, Pr=5,  S=0.2,  M=1, ω=5.0, ωt=π/2, ε=0.01

The influence of heat source parameter on visco-elastic fluid and Newtonian fluid are presented in figure 3. The introduction of heat source raises the speed of Newtonian as well non-Newtonian fluid flows. The effect of permeability on the fluid flow is shown in figure 4 and the figure characterizes that the increase of permeability parameter declines the speed of the both complex and simple fluid mechanisms along with the increasing values of visco-elastic parameter.

Figure 5: Variation of transient velocity u against y for Gr=7, Pr=5,  S=0.2,  Kp=4, ω=5.0, ωt=π/2,ε=0.01

Figure 5 illustrates the behaviour of fluid flow for various values of Hartmann number. Hartmann number depicts strength of transverse magnetic field. The application of transverse magnetic field produces Lorentz force and the Lorentz force has a retarding effect on the velocity. As a consequence, the thickness of the fluid will be enlarged and the speed will go down. This diminishing trend in speed is observed in visco-elastic fluid characterized by Walters liquid (Model B^/). The study of shearing stress experienced by the governing fluid flow gives the importance of the concerned problem. So knowing the velocity field, the shearing stress at the plate is obtained for various values of visco-elastic parameter. Figures 6-10 depict the nature of viscous drag formed during the motion of Newtonian and non-Newtonian fluids. The figures enable that the shearing stress experiences a declined trend along with the modification of visco-elastic parameter.

Figure 6: Variation of skin friction τ at the wall against Pr for Gr=7, S=0.2, Kp=4, M=1, ω=5.0, ωt=π/2, ε=0.01

Figure 6 shows the behaviour of skin friction against Prandtl number for Newtonian as well as non-Newtonian fluid flows. It is noticed that in the neighbourhood of small values of  Prandtl number, the shearing stress subdues but for Pr ≥ 2, it shows a rising trend. This phenomenon is observed in visco-elastic fluid as well as in simple Newtonian fluid.

Figure 7:  Variation of skin friction τ at the wall against Gr for  Pr=5, S=0.2, Kp=4, M=1, ω=5.0, ωt=π/2,ε=0.01

The effect of natural convection parameter on the shearing stress is analyzed in figure 7. The study of positive values of Grashof number is very important mainly because of its use in various cooling problems of engineering and industrial purposes. Here, it is detected from the figure that as the degree of coolness (Gr>0) increases, the shearing stress or viscous drag will decelerate in various fluid flow. mechanisms. But a considerable downward trend is observed for the flow governed by visco-elastic fluid in comparison to the Newtonian fluid flow.

Figure 8: Variation of skin friction τ at the wall against M for Gr=7, Pr=5, Kp=4, S=0.2, ω=5.0, ωt=π/2, ε=0.01

The effect of Lorentz force on the shearing stress is shown in figure 8 and Hartmann number characterizes the nature of Lorentz force. As Hartmann number enhances the shearing stress diminish in both Newtonian and non-Newtonian fluid flow. The influence of Hartmann number on the visco-elastic fluid flow is superior than the fluid governed by simple Newtonian law of viscosity.

Figure 9: Variation of skin friction τ at the wall against permeability parameter Kp with Gr=7, Pr=5, S=0.2, M=1, ω=5.0, ωt=π/2, ε=0.01

Figure 10: Variation of skin friction τ at the wall against S for Gr=7, Pr=5, Kp=4, M=1, ω=5.0, ωt=π/2, ε=0.01

Figure 9 and 10 represent the consequences of permeability parameter and heat source on the skin friction formed at the plate respectively. The growths of permeability parameter boost up the magnitude of skin friction along with the increasing values of visco-elastic parameter. But a reverse behaviour is experienced during the modification of strength of the heat source.

                The temperature profile and rate of heat transfer are not affected significantly during the changes made in visco-elasticity of the fluid flow.

Conclusions

From the present study we can make the following conclusions:

References

Author Biographies

Rita Choudhury Digboi (Assam), 01-11-1956. M.Sc (1978), Ph.D (1984). Specialization in Applied Mathematics, Dibrugarh University, Dibrugarh, Assam, India. Major field of study: Fluid mechanics (Non-Newtonian flow Mechanics)

Saswati Purkayastha Hojai (Assam), 12-06-1986. M.Sc (2009), M.Phil (2011). Specialization in Applied Mathematics, Gauhati University, Guwahati, Assam, India. Major field of study: Fluid mechanics.

Debasish Dey Guwahati (Assam), 05-11-1982. M.Sc (2006), Ph.D  (2012). Specialization in Applied Mathematics, Gauhati University, Guwahati, Assam, India. Major field of study: Fluid mechanics